【题目】随着科技的发展,智能制造逐渐成为一种可能的生产方式.重庆某电子零部件生产商原来采用自动化程度较低的传统生产方式,工厂有熟练工人和新工人共100人,熟练工平均每天能生产30个零件,新工人平均每天能生产20个零件,所有工人刚好用30天完成了一项7.2万个零件的生产任务.
(1)请问该工厂有熟练工,新工人各多少人?(请列二元一次方程组解题)
(2)今年,某自动化技术团队为工厂提供了A、B两种不同型号的机器人,且两种机器人都可以单独完成零件的生产.已知A型机器人的售价为80万元/台,B型机器人的售价为120万元/台.工厂准备采购价值840万元的机器人设备,两种机器人都至少购买一台,若840万元刚好用完,求出所有可能的购买方案.
(3)已知一个零件的毛利润(只扣除了原材料成本)为10元,若选择传统生产方式,熟练工每月基本工资3000元,新工人每月基本工资2000元,在基本工资之上,工厂还需额外支付计件工资5元/件,传统生产方式的设备成本忽略不计.若选择智能制造方式生产,A型机器人每月生产零件1.5万个,B型机器人每月能生产零件2.7万个,1台A型机器人需要8名技术人员操控,一台B型机器人需要12名技术人员操控,技术人员每人工资1万元,实际生产过程中,一台A型机器人平均每月的总成本为6万元(包含所有设备成本和维护成本),一台B型机器人平均每月的总成本为8万元(包含所有设备成本和维护成本).请你比较传统的生产方式和(2)中的所有购买方案对应的智能生产方式,哪种生产方式每月的总利润最大,最大利润为多少万元?(注:每月均按30天计算)
参考答案:
【答案】(1)该工厂有熟练工40名,新工人60名;(2)购买方案有三种,方案一:购买A型机器人3台,B型机器人5台;方案二:购买A型机器人6台,B型机器人3台;方案一:购买A型机器人9台,B型机器人1台;(3)选择智能制造生产方式获得利润最大,此时购进A型机器人3台,B型机器人5台,最大利润为38万元.
【解析】
(1)设有熟练工x人,新工人y人,根据熟练工人和新工人共100人,所有工人刚好用30天完成了一项7.2万个零件的生产任务,列方程组进行求解即可;
(2)设购买A型机器人a台,B型机器人b台,由题意得80a+120b=840,根据a、b均为大于1的正整数进行求解即可得;
(3)分别计算出传统方式与智能制造中的三种方案每月获得的总利润,进行比较即可.
(1)设有熟练工x人,新工人y人,由题意得
 ,
,
解得:![]() ,
,
答:该工厂有熟练工40名,新工人60名;
(2)设购买A型机器人a台,B型机器人b台,由题意得
80a+120b=840,
则a=![]() ,
,
又两种机器人都至少购买一台,
所以![]() ,即
,即 ,
,
所以1≤b≤6![]() ,
,
又![]() 为整数,
为整数,
所以b为1,3,5,
所以![]() 或
或![]() 或
或![]() ,
,
答:购买方案有三种,方案一:购买A型机器人3台,B型机器人5台;方案二:购买A型机器人6台,B型机器人3台;方案一:购买A型机器人9台,B型机器人1台;
(3)传统方式:每天生产零件:30×40+20×60=2400个,
每月生产:2400×30=720000个=7.2万个,
毛利润:7.2×10=72万元,
每月的总利润:72-40×0.3-60×0.2-7.2×5=12万元;
智能模式:方案一:生产零件:3×1.5+5×2.7=18万个,
毛利润;18×10=180万元,
每月的总利润:180-3×6-5×8-(3×8+5×12)×1=38万元;
方案二:生产零件:6×1.5+3×2.7=17.1万个,
毛利润;17.1×10=171万元,
每月的总利润:171-6×6-3×8-(6×8+3×12)×1=27万元;
方案三:生产零件:9×1.5+1×2.7=16.2万个,
毛利润;16.2×10=162万元,
每月的总利润:162-9×6-1×8-(9×8+1×12)×1=16万元,
综上,选择智能制造生产方式获得利润最大,此时购进A型机器人3台,B型机器人5台,最大利润为38万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在
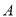 处测得灯塔
处测得灯塔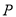 在北偏东
在北偏东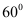 方向上,继续航行1小时到达
方向上,继续航行1小时到达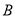 处,此时测得灯塔
处,此时测得灯塔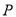 在北偏东
在北偏东 方向上.
方向上.(1)求
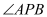 的度数;
的度数;(2)已知在灯塔
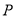 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 的一元二次方程
的一元二次方程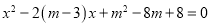
⑴说明该方程根的情况.
⑵若
 (
( 为整数),且方程有两个整数根,求
为整数),且方程有两个整数根,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△ABD中,∠BAC=∠ABD=90°,点E为AD边上的一点,且AC=AE,连接CE交AB于点G,过点A作AF⊥AD交CE于点F.
(1)求证:△AGE≌△AFC;
(2)若AB=AC,求证:AD=AF+BD.
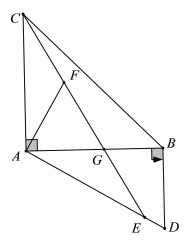
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=
 ,求
,求 的值.
的值.(3)(3分)在(2)的条件下,设⊙O的半径为3,求AB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在Rt△ABC中,∠ACB=90°,过点C作CD⊥AB于点D,点E是BC上一点,连接AE交CD于点F.
(1)如图1,若AE平分∠CAB,CP平分∠BCD,求证:FP=EP;
(2)如图2,若CE=CA,过点E作EG⊥CD于点G,点H为AE的中点,连接DH,GH,判断△GDH的形状,并证明.
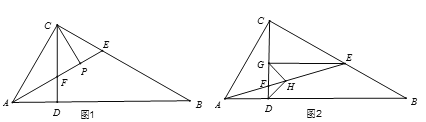
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形
 .
.(1)如图,点
 在
在 延长线上,
延长线上, ,求证:点
,求证:点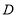 为
为 中点.
中点.
(2)如图,点
 在
在 中点,
中点, 是
是 延长线上一点,且
延长线上一点,且 ,求证:
,求证: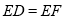 .
.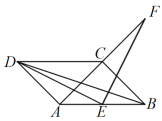
(3)在(2)的条件下,若
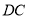 的延长线与
的延长线与 交于点
交于点 ,试判断四边形
,试判断四边形 是否为平行四边形?并证明你的结论(先补全图形再解答).
是否为平行四边形?并证明你的结论(先补全图形再解答).
相关试题

