【题目】如图,双曲线y= ![]() 经过点A(1,2),过点A作y轴的垂线,垂足为B,交双曲线y=﹣
经过点A(1,2),过点A作y轴的垂线,垂足为B,交双曲线y=﹣ ![]() 于点C,直线y=m(m≠0)分别交双曲线y=﹣
于点C,直线y=m(m≠0)分别交双曲线y=﹣ ![]() 、y=
、y= ![]() 于点P、Q.
于点P、Q.
(1)求k的值;
(2)若△OAP为直角三角形,求点P的坐标;
(3)△OCQ的面积记为S△OCQ , △OAP的面积记为S△OAP,试比较S△OCQ与S△OAP的大小(直接写出结论).
参考答案:
【答案】
(1)解:∵双曲线y= ![]() 经过点A(1,2),
经过点A(1,2),
∴k=1×2=2;
(2)解:设P(﹣ ![]() ,m),
,m),
∵A(1,2),
∴OA2=12+22=5,AP2=(1+ ![]() )2+(2﹣m)2,OP2=(
)2+(2﹣m)2,OP2=( ![]() )2+m2,
)2+m2,
当∠AOP=90°时,
∵OA2+OP2=AP2,即5+( ![]() )2+m2=(1+
)2+m2=(1+ ![]() )2+(2﹣m)2,解得m=±3,
)2+(2﹣m)2,解得m=±3,
∴P1(﹣6,3),P2(6,﹣3);
当∠OAP=90°时,
∵OA2+AP2=OP2,即5+(1+ ![]() )2+(2﹣m)2=(
)2+(2﹣m)2=( ![]() )2+m2,解得m=
)2+m2,解得m= ![]() ,
,
∴P3( ![]() ),P4(
),P4( ![]() );
);
当∠APO=90°时,此种情况不存在;
(3)解:∵A(1,2),
∴C(﹣9,2).
设P(﹣ ![]() ,m),则Q(
,m),则Q( ![]() ,m),
,m),
分别过点A、Q、P、C作x轴的垂线,垂足分别为M、N、K、H,
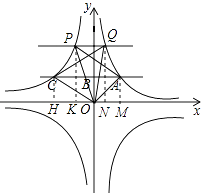
∵点A、Q在反比例函数y= ![]() 的图象上,
的图象上,
∴S△AOM=S△QON=1.
∵点C、P在反比例函数y=﹣ ![]() 的图象上,
的图象上,
∴S△COH=S△POK=9.
S△OCQ=S梯形CHNQ﹣S△COH﹣S△POK,S△OAP=S梯形AMKP﹣S△AOM﹣S△POK,
∴S△OCQ﹣S△OAP=S梯形CHNQ﹣S梯形AMKP,
∵梯形CHNQ与梯形AMKP的上底与下底相同,
∴只要比较HN与KM的大小即可,
∵HN﹣KM=(9+ ![]() )﹣(1+
)﹣(1+ ![]() )=8﹣
)=8﹣ ![]() ,
,
∴当m=±2时,HN=KM,即S△OCQ=S△OAP;
当m>2或m<﹣2时,8﹣ ![]() >0,即S△OCQ>S△OAP;
>0,即S△OCQ>S△OAP;
当﹣2<m<2时,8﹣ ![]() <0,即S△OCQ<S△OAP.
<0,即S△OCQ<S△OAP.
【解析】(1)将点A的坐标代入反比例函数解析式即可求出k的值。
(2)设出点P的坐标,根据点A、P、O的坐标,分别求出OA2、AP2、OP2,再分三种情况讨论:当∠AOP=90°时,得出OA2+OP2=AP2,建立关于m的方程,求解即可求出点P的坐标;当∠OAP=90°时,则OA2+AP2=OP2,建立关于m的方程,求解即可求出点P的坐标;当∠APO=90°时,此种情况不存在。
(3)根据点A(1,2)可得出C(﹣9,2).分别设出点P、Q的坐标,分别过点A、Q、P、C作x轴的垂线,垂足分别为M、N、K、H,再由反比例函数图像上的点的坐标特点得出△AOM、△QON、△COH、△POK的面积,然后根据S△OCQ﹣S△OAP=S梯形CHNQ﹣S梯形AMKP,由于梯形CHNQ与梯形AMKP的上底与下底相同,因此只需比较HN与KM的大小即可,从而分三种情况讨论,可求得结论。
【考点精析】解答此题的关键在于理解反比例函数的性质的相关知识,掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大,以及对三角形的面积的理解,了解三角形的面积=1/2×底×高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2 019的坐标为____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程(组)
(1)11x﹣3=x+2
(2)

(3)

(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E 、F ,连结BD 、DP ,BD与CF相交于点H. 给出下列结论:①△BDE ∽△DPE;②
 ;③DP 2=PH ·PB; ④
;③DP 2=PH ·PB; ④ 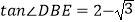 . 其中正确的是( ).
. 其中正确的是( ).
A.①②③④
B.①②④
C.②③④
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1 , 则下列结论正确的是 . (写出所有正确结论的序号)①b>0;②a-b+c<0;③阴影部分的面积为4;④若c=-1,则b2=4a.

相关试题

