【题目】解方程(组)
(1)11x﹣3=x+2
(2)![]()
(3)![]()
(4)![]()
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
【解析】
(1)根据解一元一次方程的步骤:移项、合并同类项、系数化1进行求解即可;
(2)先去分母,根据解一元一次方程的步骤求解即可;
(3)用加减消元法①×3-②×2即可求出y,把y的值代入原方程就可求出方程组的解;
(4)先去括号化简方程组,再利用加减法解方程组即可.
(1)11x﹣3=x+2
移项得:11x﹣x=3+2,
合并同类项得:10x=5,
系数化为1得:x=![]() ;
;
(2)![]()
去分母,方程的两边同时乘以6得:![]() ,
,
去括号得:![]() ,
,
合并同类项得:![]() ,
,
移项得:![]() ,
,
系数化为1得:![]() ;
;
(3)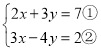
①×3-②×2得:17y=17,
解得:y=1,
把y=1代入①得:![]() ,
,
解得:x=2,
∴方程组的解为:![]() ;
;
(4)![]()
整理得: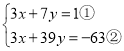
②﹣①得:32y=﹣64,
y=﹣2,
把y=﹣2代入①得:x=5,
∴方程组的解为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)按要求作图:
①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点O顺时针旋转90°得到△A2B2C2,
(2)按照(1)中②作图,回答下列问题:△A2B2C2中顶点A2坐标为 ,B2的坐标为

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2 019的坐标为____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,双曲线y=
 经过点A(1,2),过点A作y轴的垂线,垂足为B,交双曲线y=﹣
经过点A(1,2),过点A作y轴的垂线,垂足为B,交双曲线y=﹣  于点C,直线y=m(m≠0)分别交双曲线y=﹣
于点C,直线y=m(m≠0)分别交双曲线y=﹣  、y=
、y=  于点P、Q.
于点P、Q.
(1)求k的值;
(2)若△OAP为直角三角形,求点P的坐标;
(3)△OCQ的面积记为S△OCQ , △OAP的面积记为S△OAP,试比较S△OCQ与S△OAP的大小(直接写出结论). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E 、F ,连结BD 、DP ,BD与CF相交于点H. 给出下列结论:①△BDE ∽△DPE;②
 ;③DP 2=PH ·PB; ④
;③DP 2=PH ·PB; ④ 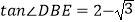 . 其中正确的是( ).
. 其中正确的是( ).
A.①②③④
B.①②④
C.②③④
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮?

相关试题

