Question

【题目】如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E 、F ，连结BD 、DP ，BD与CF相交于点H.　给出下列结论：①△BDE ∽△DPE；② ；③DP 2=PH ·PB； ④ . 其中正确的是（ ）.

A.①②③④
B.①②④
C.②③④
D.①③④

Answer 1

【答案】D
【解析】解：∵△BPC是等边三角形，

∴BP=PC=BC，∠PBC=∠PCB=∠BPC=60°，

在正方形ABCD中，

∵AB=BC=CD，∠A=∠ADC=∠BCD=90°

∴∠ABE=∠DCF=30°，

∴∠CPD=∠CDP=75°，

∴∠PDE=15°，

∵∠PBD=∠PBC-∠HBC=60°-45°=15°，

∴∠EBD=∠EDP，

∵∠DEP=∠DEB，

∴△BDE∽△DPE；

故①正确；

∵PC=CD，∠PCD=30°，

∴∠PDC=75°，

∴∠FDP=15°，

∵∠DBA=45°，

∴∠PBD=15°，

∴∠FDP=∠PBD，

∵∠DFP=∠BPC=60°，

∴△DFP∽△BPH，

∴

故②错误；

∵∠PDH=∠PCD=30°，

∵∠DPH=∠DPC，

∴△DPH∽△CDP，

∴ ，

∴PD2=PHCD，

∵PB=CD，

∴PD2=PHPB，

故③正确；

如图，过P作PM⊥CD，PN⊥BC，

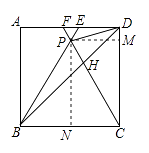
设正方形ABCD的边长是4，△BPC为正三角形，

∴∠PBC=∠PCB=60°，PB=PC=BC=CD=4，

∴∠PCD=30°

∴CM=PN=PBsin60°=4× ，PM=PCsin30°=2，

∵DE∥PM，

∴∠EDP=∠DPM，

∴∠DBE=∠DPM，

∴ ，

故④正确；

答案为：D。

①利用等边三角形的性质以及正方形的性质得出∠EPD=∠EDB=45°，再直接利用相似三角形的判定方法得出答案；
②利用等边三角形的性质结合正方形的性质证出△DFP∽△BPH，进而得出；
③利用相似三角形的判定与性质结合锐角三角函数关系得出答案；
④利用三角函数可转化 tan ∠ D B E=tan∠DPM,进而得出结果．