【题目】如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮?

参考答案:
【答案】7200元.
【解析】
连接BD.在Rt△ABD中,根据勾股定理求得BD=5,在△CBD中,由勾股定理的逆定理判定∠DBC=90°,再由S四边形ABCD=S△BAD+S△DBC求得四边形ABCD的面积,由此即可求得所需费用.
如图,连接BD.
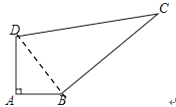
在Rt△ABD中,BD2=AB2+AD2=32+42=52,BD=5;
在△CBD中,CD2=132,BC2=122,而122+52=132,即BC2+BD2=CD2,
∴∠DBC=90°,
S四边形ABCD=S△BAD+S△DBC=![]() AD·AB+
AD·AB+![]() DB·BC=
DB·BC=![]() ×4×3+
×4×3+![]() ×5×12=36,
×5×12=36,
所以需费用36×200=7200(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程(组)
(1)11x﹣3=x+2
(2)

(3)

(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,双曲线y=
 经过点A(1,2),过点A作y轴的垂线,垂足为B,交双曲线y=﹣
经过点A(1,2),过点A作y轴的垂线,垂足为B,交双曲线y=﹣  于点C,直线y=m(m≠0)分别交双曲线y=﹣
于点C,直线y=m(m≠0)分别交双曲线y=﹣  、y=
、y=  于点P、Q.
于点P、Q.
(1)求k的值;
(2)若△OAP为直角三角形,求点P的坐标;
(3)△OCQ的面积记为S△OCQ , △OAP的面积记为S△OAP,试比较S△OCQ与S△OAP的大小(直接写出结论). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E 、F ,连结BD 、DP ,BD与CF相交于点H. 给出下列结论:①△BDE ∽△DPE;②
 ;③DP 2=PH ·PB; ④
;③DP 2=PH ·PB; ④ 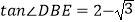 . 其中正确的是( ).
. 其中正确的是( ).
A.①②③④
B.①②④
C.②③④
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1 , 则下列结论正确的是 . (写出所有正确结论的序号)①b>0;②a-b+c<0;③阴影部分的面积为4;④若c=-1,则b2=4a.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,∠B=30°,AB≠BC ,将△ABC沿AC翻折至△AB′C ,连结B ′D. 若
 ,∠AB ′D=75°,则BC= .
,∠AB ′D=75°,则BC= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1) 定义:直角三角形两直角边的平方和等于斜边的平方.如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=__________________.
(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP=
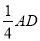 ,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.
,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.

相关试题

