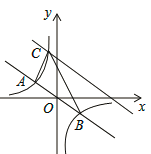
【题目】如图,在直角坐标系中,直线y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
(1)求反比例函数的表达式;
(2)将直线y=﹣![]() x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
参考答案:
【答案】(1)y=﹣![]() ;(2)y=﹣
;(2)y=﹣![]() x+8.
x+8.
【解析】
试题分析:(1)将y=3代入一次函数解析式中,求出x的值,即可得出点A的坐标,再利用反比例函数图象上点的坐标特征即可求出反比例函数的表达式;(2)根据A、B点关于原点对称,可求出点B的坐标以及线段AB的长度,设出平移后的直线的函数表达式,根据平行线间的距离公式结合三角形的面积即可得出关于b的一元一次方程,解方程即可得出结论.
试题解析:(1)令一次函数y=﹣![]() x中y=3,则3=﹣
x中y=3,则3=﹣![]() x, 解得:x=﹣6,即点A的坐标为(﹣6,3).
x, 解得:x=﹣6,即点A的坐标为(﹣6,3).
∵点A(﹣6,3)在反比例函数y=![]() 的图象上, ∴k=﹣6×3=﹣18,
的图象上, ∴k=﹣6×3=﹣18,
∴反比例函数的表达式为y=﹣![]() .
.
(2)∵A、B两点关于原点对称, ∴点B的坐标为(6,﹣3), ∴AB=![]() =6
=6![]() .
.
设平移后的直线的函数表达式为y=﹣![]() x+b(b>0),即x+2y﹣2b=0,
x+b(b>0),即x+2y﹣2b=0,
直线y=﹣![]() x可变形为x+2y=0, ∴两直线间的距离d=
x可变形为x+2y=0, ∴两直线间的距离d=![]() =
=![]() b.
b.
∴S△ABC=![]() ABd=
ABd=![]() ×6
×6![]() ×
×![]() b=48, 解得:b=8.
b=48, 解得:b=8.
∴平移后的直线的函数表达式为y=﹣![]() x+8.
x+8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班组织20名同学去春游,同时租用两种型号的车辆,一种车每辆有8个座位,另一种车每辆有4个座位,要求租用的车辆不留空座,也不能超载。租车方案有( )
A. 4种 B. 3种 C. 2种 D. 1种
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某市七年级8000人的身高情况,从中抽取800名学生的身高进行统计,下列说法不正确的是( )
A. 8000人的身高情况是总体 B. 每个学生的身高是个体
C. 800名学生身高情况是一个样本 D. 样本容量为8000人
-
科目: 来源: 题型:
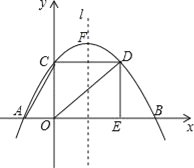
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c经过点A(﹣3,0),B(9,0)和C(0,4).CD垂直于y轴,交抛物线于点D,DE垂直与x轴,垂足为E,l是抛物线的对称轴,点F是抛物线的顶点.
(1)求出二次函数的表达式以及点D的坐标;
(2)若Rt△AOC沿x轴向右平移到其直角边OC与对称轴l重合,再沿对称轴l向上平移到点C与点F重合,得到Rt△A1O1F,求此时Rt△A1O1F与矩形OCDE重叠部分的图形的面积;
(3)若Rt△AOC沿x轴向右平移t个单位长度(0<t≤6)得到Rt△A2O2C2,Rt△A2O2C2与Rt△OED重叠部分的图形面积记为S,求S与t之间的函数表达式,并写出自变量t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标,并画出△A1B1C1;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标,并画出△A3B3C3.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在弧AB的中点,连接AF并延长与CB的延长线相交于点G,连接OF.
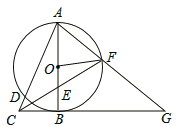
(1)求证:OF=
 BG;
BG;(2)若AB=4,求DC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种药品原价为36元/盒,经过连续两次降价后售价为25元/盒.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
A. 36(1-x)2=36-25 B. 36(1-2x)=25
C. 36(1-x)2=25 D. 36(1-x2)=25
相关试题

