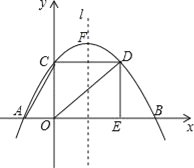
【题目】如图,已知抛物线y=ax2+bx+c经过点A(﹣3,0),B(9,0)和C(0,4).CD垂直于y轴,交抛物线于点D,DE垂直与x轴,垂足为E,l是抛物线的对称轴,点F是抛物线的顶点.
(1)求出二次函数的表达式以及点D的坐标;
(2)若Rt△AOC沿x轴向右平移到其直角边OC与对称轴l重合,再沿对称轴l向上平移到点C与点F重合,得到Rt△A1O1F,求此时Rt△A1O1F与矩形OCDE重叠部分的图形的面积;
(3)若Rt△AOC沿x轴向右平移t个单位长度(0<t≤6)得到Rt△A2O2C2,Rt△A2O2C2与Rt△OED重叠部分的图形面积记为S,求S与t之间的函数表达式,并写出自变量t的取值范围.
参考答案:
【答案】(1)D(6,4);y=﹣![]() x2+
x2+![]() x+4;(2)
x+4;(2)![]() ;(3)当0<t≤3时,S=
;(3)当0<t≤3时,S=![]() t2,当3<t≤6时,S=
t2,当3<t≤6时,S=![]() t2﹣3t+12
t2﹣3t+12
【解析】试题分析:(1)用待定系数法求抛物线解析式;(2)由GH∥A1O1,求出GH=1,再求出FH,S重叠部分=S△A1O1F﹣S△FGH计算即可;(3)分两种情况①直接用面积公式计算,②用面积差求出即可.
试题解析:(1)∵抛物线y=ax2+bx+c经过点A(﹣3,0),B(9,0)和C(0,4).
∴设抛物线的解析式为y=a(x+3)(x﹣9), ∵C(0,4)在抛物线上, ∴4=﹣27a,
∴a=﹣![]() , ∴设抛物线的解析式为y=﹣
, ∴设抛物线的解析式为y=﹣![]() (x+3)(x﹣9)=﹣
(x+3)(x﹣9)=﹣![]() x2+
x2+![]() x+4,
x+4,
∵CD垂直于y轴,C(0,4) ∴﹣![]() x2+
x2+![]() x+4=4, ∴x=6, ∵D(6,4),
x+4=4, ∴x=6, ∵D(6,4),
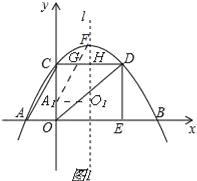
(2)如图1, ∵点F是抛物线y=﹣![]() x2+
x2+![]() x+4的顶点,∴F(3,
x+4的顶点,∴F(3,![]() ), ∴FH=
), ∴FH=![]() ,
,
∵GH∥A1O1, ∴![]() , ∴
, ∴![]() , ∴GH=1,
, ∴GH=1,
∵Rt△A1O1F与矩形OCDE重叠部分是梯形A1O1HG,
∴S重叠部分=S△A1O1F﹣S△FGH=![]()
![]() A1O1×O1F﹣
A1O1×O1F﹣![]()
![]() GH×FH=
GH×FH=![]() ×3×4﹣
×3×4﹣![]() ×1×
×1×![]() =
=![]() .
.
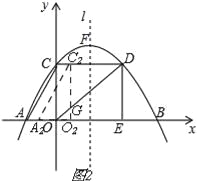
(3)①当0<t≤3时,如图2, ∵C2O2∥DE, ∴![]() , ∴
, ∴![]() , ∴O2G=
, ∴O2G=![]() t,
t,
∴S=S△OO2G=![]() OO2×O2G=
OO2×O2G=![]() t×
t×![]() t=
t=![]() t2,
t2,
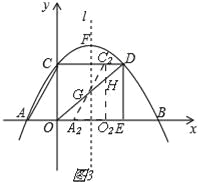
②当3<t≤6时,如图3, ∵C2H∥OC, ∴![]() , ∴
, ∴![]() , ∴C2H=
, ∴C2H=![]() (6﹣t),
(6﹣t),
∴S=S四边形A2O2HG=S△A2O2C2﹣S△C2GH=![]() OA×OC﹣
OA×OC﹣![]() C2H×(t﹣3)=
C2H×(t﹣3)=![]() ×3×4﹣
×3×4﹣![]() ×
×![]() (6﹣t)(t﹣3)=
(6﹣t)(t﹣3)=![]() t2﹣3t+12
t2﹣3t+12
∴当0<t≤3时,S=![]() t2,当3<t≤6时,S=
t2,当3<t≤6时,S=![]() t2﹣3t+12.
t2﹣3t+12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的多项式(a-b)x4+(b-1)x3-(a-2)x2+ax-4不含x3与x2项,试写出这个多项式,并求出当x=-2时,这个多项式的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班组织20名同学去春游,同时租用两种型号的车辆,一种车每辆有8个座位,另一种车每辆有4个座位,要求租用的车辆不留空座,也不能超载。租车方案有( )
A. 4种 B. 3种 C. 2种 D. 1种
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某市七年级8000人的身高情况,从中抽取800名学生的身高进行统计,下列说法不正确的是( )
A. 8000人的身高情况是总体 B. 每个学生的身高是个体
C. 800名学生身高情况是一个样本 D. 样本容量为8000人
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线y=﹣
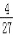 x与反比例函数y=
x与反比例函数y=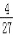 的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.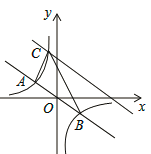
(1)求反比例函数的表达式;
(2)将直线y=﹣
 x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标,并画出△A1B1C1;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标,并画出△A3B3C3.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在弧AB的中点,连接AF并延长与CB的延长线相交于点G,连接OF.
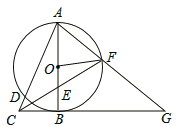
(1)求证:OF=
 BG;
BG;(2)若AB=4,求DC的长.
相关试题

