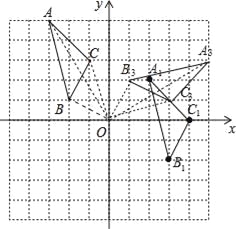
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标,并画出△A1B1C1;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标,并画出△A3B3C3.

参考答案:
【答案】(1)图形见解析;A1的坐标为(2,2),B1点的坐标为(3,﹣2);(2)图形见解析;A2(3,﹣5),B2(2,﹣1),C2(1,﹣3);(3)图形见解析;A3(5,3),B3(1,2),C3(3,1).
【解析】试题分析:(1)利用点C和点C1的坐标变化得到平移的方向与距离,然后利用此平移规律写出顶点A1,B1的坐标;
(2)根据关于原点对称的点的坐标特征求解;
(3)利用网格和旋转的性质画出△A2B3C3,然后写出△A2B3C3的各顶点的坐标.
试题解析:(1)如图,△A1B1C1为所作,
因为点C(﹣1,3)平移后的对应点C1的坐标为(4,0),
所以△ABC先向右平移5个单位,再向下平移3个单位得到△A1B1C1,
所以点A1的坐标为(2,2),B1点的坐标为(3,﹣2);
(2)因为△ABC和△A1B2C2关于原点O成中心对称图形,
所以A2(3,﹣5),B2(2,﹣1),C2(1,﹣3);
(3)如图,△A2B3C3为所作,A3(5,3),B3(1,2),C3(3,1);
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某市七年级8000人的身高情况,从中抽取800名学生的身高进行统计,下列说法不正确的是( )
A. 8000人的身高情况是总体 B. 每个学生的身高是个体
C. 800名学生身高情况是一个样本 D. 样本容量为8000人
-
科目: 来源: 题型:
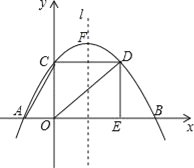
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c经过点A(﹣3,0),B(9,0)和C(0,4).CD垂直于y轴,交抛物线于点D,DE垂直与x轴,垂足为E,l是抛物线的对称轴,点F是抛物线的顶点.
(1)求出二次函数的表达式以及点D的坐标;
(2)若Rt△AOC沿x轴向右平移到其直角边OC与对称轴l重合,再沿对称轴l向上平移到点C与点F重合,得到Rt△A1O1F,求此时Rt△A1O1F与矩形OCDE重叠部分的图形的面积;
(3)若Rt△AOC沿x轴向右平移t个单位长度(0<t≤6)得到Rt△A2O2C2,Rt△A2O2C2与Rt△OED重叠部分的图形面积记为S,求S与t之间的函数表达式,并写出自变量t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线y=﹣
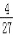 x与反比例函数y=
x与反比例函数y=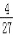 的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.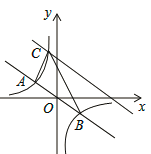
(1)求反比例函数的表达式;
(2)将直线y=﹣
 x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在弧AB的中点,连接AF并延长与CB的延长线相交于点G,连接OF.
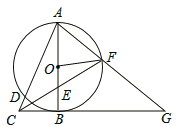
(1)求证:OF=
 BG;
BG;(2)若AB=4,求DC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种药品原价为36元/盒,经过连续两次降价后售价为25元/盒.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
A. 36(1-x)2=36-25 B. 36(1-2x)=25
C. 36(1-x)2=25 D. 36(1-x2)=25
-
科目: 来源: 题型:
查看答案和解析>>【题目】用语言叙述多项式“-a-3”所表示的数量关系,下列叙述正确的是( )
A. a与-3的和
B. a的相反数与3的差
C. a的相反数与3的和
D. a的相反数与-3的差
相关试题

