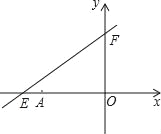
【题目】如图,直线y=kx+6分别与x轴、y轴交于点E,F,已知点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值;
(2)若点P(x,y)是该直线上的一个动点,且在第二象限内运动,试写出△OPA的面积S关于x的函数解析式,并写出自变量x的取值范围.
(3)探究:当点P运动到什么位置时,△OPA的面积为![]() ,并说明理由.
,并说明理由.
参考答案:
【答案】(1)k=![]() ;(2)△OPA的面积S=
;(2)△OPA的面积S=![]() x+18 (﹣8<x<0);(3)点P坐标为(
x+18 (﹣8<x<0);(3)点P坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )时,三角形OPA的面积为
)时,三角形OPA的面积为![]() .
.
【解析】
(1)将点E坐标(﹣8,0)代入直线y=kx+6就可以求出k值,从而求出直线的解析式;
(2)由点A的坐标为(﹣6,0)可以求出OA=6,求△OPA的面积时,可看作以OA为底边,高是P点的纵坐标的绝对值.再根据三角形的面积公式就可以表示出△OPA.从而求出其关系式;根据P点的移动范围就可以求出x的取值范围.
(3)分点P在x轴上方与下方两种情况分别求解即可得.
(1)∵直线y=kx+6过点E(﹣8,0),
∴0=﹣8k+6,
k=![]() ;
;
(2)∵点A的坐标为(﹣6,0),
∴OA=6,
∵点P(x,y)是第二象限内的直线上的一个动点,
∴△OPA的面积S=![]() ×6×(
×6×(![]() x+6)=
x+6)=![]() x+18 (﹣8<x<0);
x+18 (﹣8<x<0);
(3)设点P的坐标为(m,n),则有S△AOP=![]() ,
,
即![]() ,
,
解得:n=±![]() ,
,
当n=![]() 时,
时,![]() =
=![]() x+6,解得x=
x+6,解得x=![]() ,
,
此时点P在x轴上方,其坐标为(![]() ,
,![]() );
);
当n=-![]() 时,-
时,-![]() =
=![]() x+6,解得x=
x+6,解得x=![]() ,
,
此时点P在x轴下方,其坐标为(![]() ,
,![]() ),
),
综上,点P坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某区九年级学生身体素质情况,该区从全区九年级学生中随机抽取了部分学生进行了一次体育考试科目测试(把测试结果分为四个等级:A级:优秀:B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如图两幅不完整的统计图.请根据统计图中的信息解答下列问题:

(1)本次抽样测试的学生是;
(2)求图1中∠α的度数是°,把图2条形统计图补充完整;
(3)该区九年级有学生3500名,如果全部参加这次体育科目测试,请估计不及格的人数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连结OC,若∠AOC=125°,则∠ABC= .
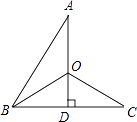
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,圆规两脚形成的角α称为圆规的张角.一个圆规两脚均为12cm,最大张角150°,你能否画出一个半径为20cm的圆?请借助图2说明理由.(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1⊥x轴于点A(2,0),点B是直线l1上的动点.直线l2:y=x+1交l1于点C,过点B作直线l3垂直于l2 , 垂足为D,过点O,B的直线l4交l2于点E,当直线l1 , l2 , l3能围成三角形时,设该三角形面积为S1 , 当直线l2 , l3 , l4能围成三角形时,设该三角形面积为S2 .

(1)若点B在线段AC上,且S1=S2 , 则B点坐标为;
(2)若点B在直线l1上,且S2= S1 , 则∠BOA的度数为 .
S1 , 则∠BOA的度数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸拼成如图2的等腰梯形,
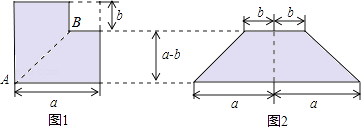
(1)设图1中阴影部分面积为S1 , 图2中阴影部分面积为S2 , 请直接用含a、b的代数式表示S1和S2;
(2)请写出上述过程所揭示的乘法公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在义乌市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为:“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图.

请你结合图中信息,解答下列问题:
(1)本次共调查了名学生;
(2)被调查的学生中,最喜爱丁类图书的学生有人,最喜爱甲类图书的人数占本次被调查人数的%;
(3)在最喜爱丙类图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生1500人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人?
相关试题

