【题目】在义乌市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为:“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图. 
请你结合图中信息,解答下列问题:
(1)本次共调查了名学生;
(2)被调查的学生中,最喜爱丁类图书的学生有人,最喜爱甲类图书的人数占本次被调查人数的%;
(3)在最喜爱丙类图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生1500人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人?
参考答案:
【答案】
(1)200
(2)15;40
(3)解:设男生人数为x人,则女生人数为1.5x人,由题意得:
x+1.5x=1500×20%,
解得:x=120,
当x=120时,1.5x=180.
答:该校最喜爱丙类图书的女生和男生分别有180人,120人
【解析】解:(1)共调查的学生数:40÷20%=200(人);(2)最喜爱丁类图书的学生数:200﹣80﹣65﹣40=15(人);最喜爱甲类图书的人数所占百分比:80÷200×100%=40%;
【考点精析】利用扇形统计图和条形统计图对题目进行判断即可得到答案,需要熟知能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+6分别与x轴、y轴交于点E,F,已知点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值;
(2)若点P(x,y)是该直线上的一个动点,且在第二象限内运动,试写出△OPA的面积S关于x的函数解析式,并写出自变量x的取值范围.
(3)探究:当点P运动到什么位置时,△OPA的面积为
 ,并说明理由.
,并说明理由.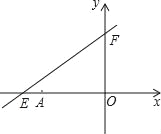
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1⊥x轴于点A(2,0),点B是直线l1上的动点.直线l2:y=x+1交l1于点C,过点B作直线l3垂直于l2 , 垂足为D,过点O,B的直线l4交l2于点E,当直线l1 , l2 , l3能围成三角形时,设该三角形面积为S1 , 当直线l2 , l3 , l4能围成三角形时,设该三角形面积为S2 .

(1)若点B在线段AC上,且S1=S2 , 则B点坐标为;
(2)若点B在直线l1上,且S2= S1 , 则∠BOA的度数为 .
S1 , 则∠BOA的度数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸拼成如图2的等腰梯形,
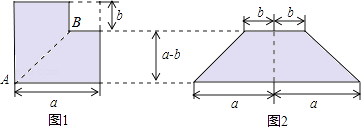
(1)设图1中阴影部分面积为S1 , 图2中阴影部分面积为S2 , 请直接用含a、b的代数式表示S1和S2;
(2)请写出上述过程所揭示的乘法公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣
 x﹣
x﹣ 交x轴于点A,交y轴于点C,直线y=
交x轴于点A,交y轴于点C,直线y=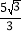 x﹣5
x﹣5 交x轴于点B,在平面内有一点E,其坐标为(4,
交x轴于点B,在平面内有一点E,其坐标为(4,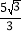 ),连接CB,点K是线段CB的中点,另有两点M,N,其坐标分别为(a,0),(a+1,0).将K点先向左平移
),连接CB,点K是线段CB的中点,另有两点M,N,其坐标分别为(a,0),(a+1,0).将K点先向左平移 个单位,再向上平移
个单位,再向上平移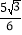 个单位得K′,当以K′,E,M,N四点为顶点的四边形周长最短时,a的值为_____.
个单位得K′,当以K′,E,M,N四点为顶点的四边形周长最短时,a的值为_____.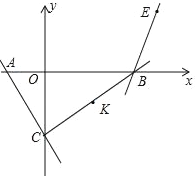
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.

(1)若⊙O的半径为8,求CD的长;
(2)证明:PE=PF;
(3)若PF=13,sinA=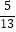 ,求EF的长.
,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
采购数量(件)
1
2
…
A产品单价(元/件)
1480
1460
…
B产品单价(元/件)
1290
1280
…
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的 ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.
相关试题

