【题目】某种油菜籽在相同条件下的发芽实验结果如表:
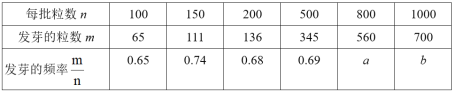
(1)a= ,b= ;
(2)这种油菜籽发芽的概率估计值是多少?请简要说明理由;
(3)如果该种油菜籽发芽后的成秧率为90%,则在相同条件下用10000粒该种油菜籽可得到油菜秧苗多少棵?
参考答案:
【答案】(1)0.70,0.70;(2)0.70,理由见解析;(3)6300棵.
【解析】
(1)用发芽的粒数m![]() 每批粒数n即可得到发芽的频率
每批粒数n即可得到发芽的频率![]() ;
;
(2)6批次种子粒数从100粒逐渐增加到1000粒时,种子发芽的频率趋近于![]() ,所以估计当n很大时,频率将接近
,所以估计当n很大时,频率将接近![]() ,由此即可得出答案;
,由此即可得出答案;
(3)首先计算发芽的种子数,然后乘以![]() 即可得.
即可得.
(1)![]() ,
,![]()
故答案为:![]() ,
,![]() ;
;
(2)这种油菜籽发芽的概率估计值是![]()
理由:由表可知,这6批次种子粒数从100粒逐渐增加到1000粒时,种子发芽的频率趋近于![]() ,则种子发芽的频率为
,则种子发芽的频率为![]()
由频率估计概率可得:这种油菜籽发芽的概率估计值是![]() ;
;
(3)这种油菜籽发芽的种子数为![]() (粒)
(粒)
则![]() (棵)
(棵)
答:在相同条件下用10000粒该种油菜籽可得到油菜秧苗6300棵.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把顺次连接四边形各边中点所得的四边形叫做中点四边形.若一个任意四边形的面积为a,则它的中点四边形面积为( )
A.
 aB.
aB.  C.
C. D.
D.
-
科目: 来源: 题型:
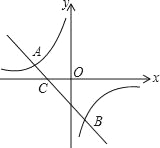
查看答案和解析>>【题目】如图,已知A(﹣4,2),B(n,﹣4)是一次函数y=kx+b的图象与反比例函数
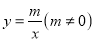 的图象的两个交点.
的图象的两个交点.(1)求反比例函数和一次函数的表达式;
(2)根据图象写出使一次函数的函数值小于反比例函数的函数值的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数
 (x<0)与y=ax+b的图象交于点A(﹣1,n)和点B(﹣2,1).
(x<0)与y=ax+b的图象交于点A(﹣1,n)和点B(﹣2,1).(1)求k,a,b的值;
(2)直线x=m与
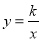 (x<0)的图象交于点P,与y=﹣x+1的图象交于点Q,当∠PAQ>90°时,直接写出m的取值范围.
(x<0)的图象交于点P,与y=﹣x+1的图象交于点Q,当∠PAQ>90°时,直接写出m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax+b(a≠0)的图象与反比例函数
 (k≠0)的图象相交于A,B两点,与x轴,y轴分别交于C,D两点,tan∠DCO=
(k≠0)的图象相交于A,B两点,与x轴,y轴分别交于C,D两点,tan∠DCO= ,过点A作AE⊥x轴于点E,若点C是OE的中点,且点A的横坐标为﹣4.,
,过点A作AE⊥x轴于点E,若点C是OE的中点,且点A的横坐标为﹣4.,(1)求该反比例函数和一次函数的解析式;
(2)连接ED,求△ADE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD关于y轴对称,边AD在x轴上,点B在第四象限,直线BD与反比例函数
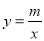 的图象交于点B、E.
的图象交于点B、E.(1)求反比例函数及直线BD的解析式;
(2)求点E的坐标.
-
科目: 来源: 题型:
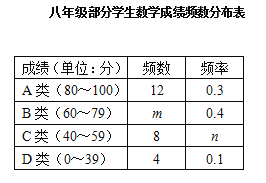
查看答案和解析>>【题目】某中学八年级共有10个班,每班40名学生,学校对该年级学生数学学科某次学情调研测试成绩进行了抽样分析,请按要求回答下列问题:
(1)若要从全年级学生中抽取40人进行调查,你认为以下抽样方法中最合理的是 .
①随机抽取一个班级的40名学生的成绩;
②在八年级学生中随机抽取40名女学生的成绩;
③在八年级10个班中每班各随机抽取4名学生的成绩.
(2)将抽取的40名学生的成绩进行分组,绘制如下成绩频数分布表:
①m= ,n= ;
②根据表格中的数据,请用扇形统计图表示学生成绩分布情况.
相关试题

