【题目】如图,函数![]() (x<0)与y=ax+b的图象交于点A(﹣1,n)和点B(﹣2,1).
(x<0)与y=ax+b的图象交于点A(﹣1,n)和点B(﹣2,1).
(1)求k,a,b的值;
(2)直线x=m与![]() (x<0)的图象交于点P,与y=﹣x+1的图象交于点Q,当∠PAQ>90°时,直接写出m的取值范围.
(x<0)的图象交于点P,与y=﹣x+1的图象交于点Q,当∠PAQ>90°时,直接写出m的取值范围.

参考答案:
【答案】(1)k=﹣2,a=1,b=3;(2)当m<﹣2或﹣1<m<0时,∠PAQ>90°.
【解析】试题分析:
(1)把点B的坐标代入![]() 即可求得k的值;再把点A的坐标代入所得反比例函数的解析式即可求得n的值;把A、B的坐标代入一次函数
即可求得k的值;再把点A的坐标代入所得反比例函数的解析式即可求得n的值;把A、B的坐标代入一次函数![]() 列出方程组,解方程组即可求得a、b的值;
列出方程组,解方程组即可求得a、b的值;
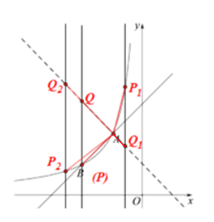
(2)如下图,由(1)可知一次函数![]() 的解析式为:
的解析式为: ![]() ,点A的坐标为(-1,2),由此可得:直线
,点A的坐标为(-1,2),由此可得:直线![]() 过点A,且直线
过点A,且直线![]() 垂直于直线
垂直于直线![]() ,垂足为点A,即∠QAB=90°,由下图可知,①当直线
,垂足为点A,即∠QAB=90°,由下图可知,①当直线![]() 在点B的左侧时,∠PAQ<90°;②当直线
在点B的左侧时,∠PAQ<90°;②当直线![]() 过点B时,∠PAQ=90°;③当直线
过点B时,∠PAQ=90°;③当直线![]() 在点B的右侧,点A左侧时,∠PAQ>90°;④当直线
在点B的右侧,点A左侧时,∠PAQ>90°;④当直线![]() 过点A时,P、A、Q三点重合;⑤当直线
过点A时,P、A、Q三点重合;⑤当直线![]() 在点A右侧,原点左侧时,∠P1AQ1>90°.综合可得当
在点A右侧,原点左侧时,∠P1AQ1>90°.综合可得当![]() ,且
,且![]() 时,∠PAQ>90°.
时,∠PAQ>90°.
试题解析:
(1)∵ 函数![]() (
(![]() )的图象经过点B(-2, 1),
)的图象经过点B(-2, 1),
∴![]() ,得
,得![]() .
.
∵ 函数![]() (
(![]() )的图象还经过点A(-1,n),
)的图象还经过点A(-1,n),
∴![]() ,点A的坐标为(-1,2).
,点A的坐标为(-1,2).
∵ 函数![]() 的图象经过点A和点B,
的图象经过点A和点B,
∴![]() 解得
解得![]()
(2)如下图,由(1)可知一次函数![]() 的解析式为:
的解析式为: ![]() ,点A的坐标为(-1,2),
,点A的坐标为(-1,2),
∴直线![]() 过点A,且直线
过点A,且直线![]() 垂直于直线
垂直于直线![]() ,垂足为点A,
,垂足为点A,
∴∠QAB=90°,
结合图形和已知条件分析可知,∠QAB的大小存在以下情形:①当直线![]() 在点B的左侧时,∠P2AQ2<90°;②当直线
在点B的左侧时,∠P2AQ2<90°;②当直线![]() 过点B时,∠PAQ=90°;③当直线
过点B时,∠PAQ=90°;③当直线![]() 在点B的右侧,点A左侧时,∠PAQ>90°;④当直线
在点B的右侧,点A左侧时,∠PAQ>90°;④当直线![]() 过点A时,P、A、Q三点重合;⑤当直线
过点A时,P、A、Q三点重合;⑤当直线![]() 在点A右侧,原点左侧时,∠P1AQ1>90°;
在点A右侧,原点左侧时,∠P1AQ1>90°;
综上所述,当![]() 且
且![]() 时,∠PAQ>90°.
时,∠PAQ>90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年3月25日是全国中小学生安全教育日,某中学为加强学生的安全意识,组织了全校800名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图解题.


(1)这次抽取了 名学生的竞赛成绩进行统计,其中:m= ,n=
(2)补全频数分布直方图.
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B
 90°,AB
90°,AB 4,BC
4,BC 2,以AC为边作△ACE,∠ACE
2,以AC为边作△ACE,∠ACE 90°,AC=CE,延长BC至点D,使CD
90°,AC=CE,延长BC至点D,使CD 5,连接DE.求证:△ABC∽△CED.
5,连接DE.求证:△ABC∽△CED.
-
科目: 来源: 题型:
查看答案和解析>>【题目】古代阿拉伯数学家泰比特·伊本·奎拉对勾股定理进行了推广研究:如图(图1中
 为锐角,图2中
为锐角,图2中 为直角,图3中
为直角,图3中 为钝角).
为钝角).
在△ABC的边BC上取
 ,
,  两点,使
两点,使 ,则
,则 ∽
∽ ∽
∽ ,
,  ,
,  ,进而可得
,进而可得
 ;(用
;(用 表示)
表示)若AB=4,AC=3,BC=6,则

 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B,C三点在⊙O上,直径BD平分∠ABC,过点D作DE∥AB交弦BC于点E,在BC的延长线上取一点F,使得EF
 DE.
DE.(1)求证:DF是⊙O的切线;
(2)连接AF交DE于点M,若 AD
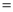 4,DE
4,DE 5,求DM的长.
5,求DM的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】画图,探究:
(1)一个正方体组合图形的主视图、左视图(如图1)所示.
①这个几何体可能是(图2)甲、乙中的 ;
②这个几何体最多可由 个小正方体构成,请在图3中画出符合最多情况的一个俯视图.
(2)如图,已知一平面内的四个点A、B、C、D,根据要求用直尺画图.
①画线段AB,射线AD;
②找一点M,使M点即在射线AD上,又在直线BC上;
③找一点N,使N到A、B、C、D四个点的距离和最短.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,
 ,
,  °,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至
°,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至 ,连接
,连接 .已知AB
.已知AB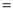 2cm,设BD为x cm,B
2cm,设BD为x cm,B 为y cm.
为y cm.
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整.(说明:解答中所填数值均保留一位小数)
(1)通过取点、画图、测量,得到了
 与
与 的几组值,如下表:
的几组值,如下表: 

0.5
0.7
1.0
1.5
2.0
2.3
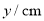
1.7
1.3
1.1
0.7
0.9
1.1
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:
线段
 的长度的最小值约为__________
的长度的最小值约为__________  ;
;若

 ,则
,则 的长度x的取值范围是_____________.
的长度x的取值范围是_____________.
相关试题

