【题目】在△ABC中,已知∠B-∠A=5°,∠C-∠B=20°,求三角形各内角的度数.
参考答案:
【答案】∠A=50°,∠B=55°,∠C=75.
【解析】
根据等量关系与三角形的内角和即可求解.
∵∠B-∠A=5°,∠C-∠B=20°,
即∠A=∠B-5°, ∠C =∠B +20°,
又∠A+∠B+∠C=180°,
∴∠B-5°+∠B+∠B +20°=180° ,
解得∠B=55°
∴∠A=50°,∠B=55°,∠C=75°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】算术平方根和立方根都等于本身的数有 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】16的算术平方根是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣4x+2=0的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
-
科目: 来源: 题型:
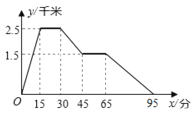
查看答案和解析>>【题目】如图所示:图象中所反映的过程是:小冬从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x轴表示时间,y轴表示小冬离家的距离.根据图象提供的信息,下列说法正确的有________.
①.体育场离小冬家2.5千米 ②.小冬在体育场锻炼了15分钟
③.体育场离早餐店4千米 ④.小冬从早餐店回家的平均速度是3千米/小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)发现
如图,点
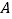 为线段
为线段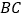 外一动点,且
外一动点,且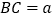 ,
,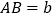 .
.填空:当点
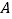 位于____________时,线段
位于____________时,线段 的长取得最大值,且最大值为_________.(用含
的长取得最大值,且最大值为_________.(用含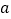 ,
,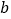 的式子表示)
的式子表示)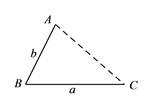
(2)应用
点
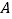 为线段
为线段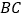 外一动点,且
外一动点,且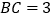 ,
, .如图所示,分别以
.如图所示,分别以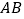 ,
, 为边,作等边三角形
为边,作等边三角形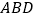 和等边三角形
和等边三角形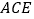 ,连接
,连接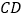 ,
,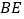 .
.①找出图中与
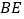 相等的线段,并说明理由;
相等的线段,并说明理由;②直接写出线段
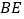 长的最大值.
长的最大值.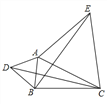
(3)拓展
如图,在平面直角坐标系中,点
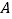 的坐标为
的坐标为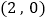 ,点
,点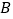 的坐标为
的坐标为 ,点
,点 为线段
为线段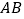 外一动点,且
外一动点,且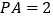 ,
,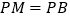 ,
,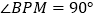 ,求线段
,求线段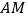 长的最大值及此时点
长的最大值及此时点 的坐标.
的坐标.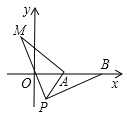
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
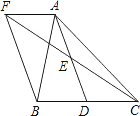
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
相关试题

