【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
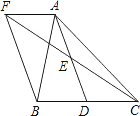
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
参考答案:
【答案】(1)证明见解析;(2)四边形AFBD是矩形.理由见解析.
【解析】
试题分析:(1)先由AF∥BC,利用平行线的性质可证∠AFE=∠DCE,而E是AD中点,那么AE=DE,∠AEF=∠DEC,利用AAS可证△AEF≌△DEC,那么有AF=DC,又AF=BD,从而有BD=CD;
(2)四边形AFBD是矩形.由于AF平行等于BD,易得四边形AFBD是平行四边形,又AB=AC,BD=CD,利用等腰三角形三线合一定理,可知AD⊥BC,即∠ADB=90°,那么可证四边形AFBD是矩形.
试题分析:(1)∵AF∥BC,
∴∠AFE=∠DCE,
∵E是AD的中点,
∴AE=DE,
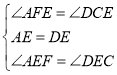 ,
,
∴△AEF≌△DEC(AAS),
∴AF=DC,
∵AF=BD,
∴BD=CD;
(2)四边形AFBD是矩形.
理由:
∵AB=AC,D是BC的中点,
∴AD⊥BC,
∴∠ADB=90°
∵AF=BD,
∵过A点作BC的平行线交CE的延长线于点F,即AF∥BC,
∴四边形AFBD是平行四边形,
又∵∠ADB=90°,
∴四边形AFBD是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,已知∠B-∠A=5°,∠C-∠B=20°,求三角形各内角的度数.
-
科目: 来源: 题型:
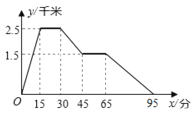
查看答案和解析>>【题目】如图所示:图象中所反映的过程是:小冬从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x轴表示时间,y轴表示小冬离家的距离.根据图象提供的信息,下列说法正确的有________.
①.体育场离小冬家2.5千米 ②.小冬在体育场锻炼了15分钟
③.体育场离早餐店4千米 ④.小冬从早餐店回家的平均速度是3千米/小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)发现
如图,点
 为线段
为线段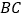 外一动点,且
外一动点,且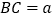 ,
,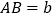 .
.填空:当点
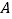 位于____________时,线段
位于____________时,线段 的长取得最大值,且最大值为_________.(用含
的长取得最大值,且最大值为_________.(用含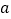 ,
,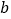 的式子表示)
的式子表示)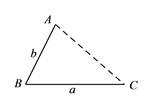
(2)应用
点
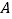 为线段
为线段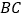 外一动点,且
外一动点,且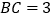 ,
, .如图所示,分别以
.如图所示,分别以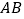 ,
, 为边,作等边三角形
为边,作等边三角形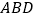 和等边三角形
和等边三角形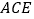 ,连接
,连接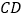 ,
,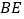 .
.①找出图中与
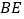 相等的线段,并说明理由;
相等的线段,并说明理由;②直接写出线段
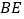 长的最大值.
长的最大值.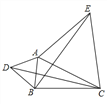
(3)拓展
如图,在平面直角坐标系中,点
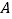 的坐标为
的坐标为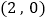 ,点
,点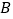 的坐标为
的坐标为 ,点
,点 为线段
为线段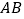 外一动点,且
外一动点,且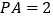 ,
,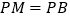 ,
,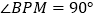 ,求线段
,求线段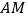 长的最大值及此时点
长的最大值及此时点 的坐标.
的坐标.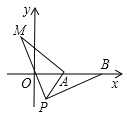
-
科目: 来源: 题型:
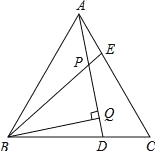
查看答案和解析>>【题目】已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,
求证:BP=2PQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AGF=∠ABC,∠1+∠2=180°,
(1)求证;BF∥DE.
(2)如果DE⊥AC于点E,∠2=150°,求∠AFG的度数.

-
科目: 来源: 题型:
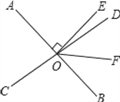
查看答案和解析>>【题目】如图,直线AB、CD相交于O点,∠AOC与∠AOD的度数比为4:5,OE⊥AB于点O,OF平分∠DOB,求∠EOF的度数
相关试题

