【题目】如图,已知O为直线AD上一点,∠AOC与∠AOB互补,OM和ON分别是∠AOC和∠AOB的平分线.
(1) 试说明:∠AOB=∠COD;
(2) 若∠COD=36°,求∠MON的度数.
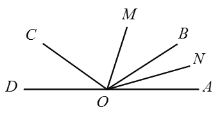
参考答案:
【答案】(1)证明过程见解析;(2)54°。
【解析】
(1)根据题目可知∠AOC与∠AOB互补,∠AOC与∠COD互补,再利用等量代换即可求证该结论.
(2)根据∠COD=36°,可以求出∠AOC和∠AOB的度数,再由OM和ON分别是∠AOC和∠AOB的平分线,可以求出∠MOA和∠BON的度数,进而求出∠MON的度数.
(1)∵O为直线AD上一点
∴∠COD+∠AOC=180°
又∵∠AOC与∠AOB互补
∴∠AOC+∠AOB=180°
∴∠AOB=∠COD(等量代换).
(2)∵∠COD=36°
由(1)可知∠AOB=∠COD=36°
∠AOC=180°-∠COD=180°-36°=144°
又∵OM和ON分别是∠AOC和∠AOB的平分线
∴∠MOA=![]() ∠AOC=72°,∠BON=
∠AOC=72°,∠BON=![]() ∠AOBA=18°
∠AOBA=18°
∴∠MON=∠MOA-∠BON=72°-18°=54°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线AB与x轴、y轴相交于
 、
、 两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转
两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转 得到CD,当点D恰好落在直线AB上时,过点D作
得到CD,当点D恰好落在直线AB上时,过点D作 轴于点E.
轴于点E.
(1)求证,
 ;
;(2)如图2,将
 沿x轴正方向平移得
沿x轴正方向平移得 ,当直线
,当直线 经过点D时,求点D的坐标及
经过点D时,求点D的坐标及 平移的距离;
平移的距离;
(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠AOB=90°,点C、D分别在射线OA、OB上,点E在∠AOB内部.
(1)根据语句画图形:
①画直线CE;
②画射线OE;
③画线段DE,
(2)结合图形,完成下面的填空:
①与∠ODE互补的角是 ;
②若∠BOE =
 ∠AOE,则∠BOE的大小是 .
∠AOE,则∠BOE的大小是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表,根据相关信息完成下列问题:
(1)统计表中的
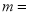 ,
,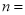 ;
;(2)扇形统计图中“C组”所对应的圆心角的度数是 ;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.

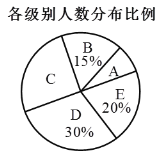
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着科技的进步和网络资源的丰富,在线学习已成为更多人的自主学习选择,某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论,为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
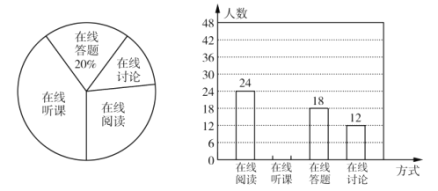
根据图中信息,解答下列问题:
(1)求本次调查的学生总人数,并通过计算补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生1800人,请你估计该校对在线阅读最感兴趣的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
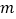 、
、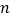 满足:
满足: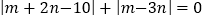 .
.(1)求
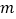 、
、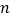 的值;
的值;(2)已知线段AB=
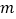 ,点P在直线AB上,且
,点P在直线AB上,且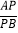 =
=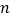 ,点Q为PB的中点,求线段AQ的长.
,点Q为PB的中点,求线段AQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有除颜色外都相同的红球和黄球,两种颜色的球一共有10个,每次摸出其中一个球,记下颜色后,放回搅匀.一个同学进行了反复试验,下面是做该试验获得的数据.
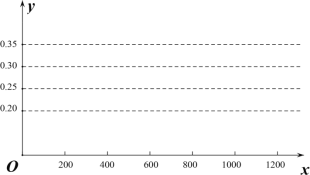
(1)a= ,画出摸到红球的频率的折线统计图;
(2)从这个袋子中任意摸一个球,摸到黄球的概率估计值是多少?(精确到0.1)
(3)怎样改变袋中红球或黄球的个数,可以使得任意摸一次,摸到两种颜色球的概率相等?(写出一种方案即可)
相关试题

