【题目】如图1,在平面直角坐标系中,直线AB与x轴、y轴相交于![]() 、
、![]() 两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转
两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转![]() 得到CD,当点D恰好落在直线AB上时,过点D作
得到CD,当点D恰好落在直线AB上时,过点D作![]() 轴于点E.
轴于点E.

(1)求证,![]() ;
;
(2)如图2,将![]() 沿x轴正方向平移得
沿x轴正方向平移得![]() ,当直线
,当直线![]() 经过点D时,求点D的坐标及
经过点D时,求点D的坐标及![]() 平移的距离;
平移的距离;

(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标,若不存在,请说明理由.
参考答案:
【答案】(1)![]() ,见解析;(2)D(3,1),
,见解析;(2)D(3,1),![]() 平移的距离是
平移的距离是![]() 个单位,见解析;(3)存在满足条件的点Q,其坐标为
个单位,见解析;(3)存在满足条件的点Q,其坐标为![]() 或
或![]() 或
或![]() ,见解析.
,见解析.
【解析】
(1)根据AAS或ASA即可证明;
(2)首先求直线AB的解析式,再求出出点D的坐标,再求出直线B′C′的解析式,求出点C′的坐标即可解决问题;
(3)如图3中,作CP∥AB交y轴于P,作PQ∥CD交AB于Q,则四边形PCDQ是平行四边形,求出直线PC的解析式,可得点P坐标,点C向左平移1个单位,向上平移![]() 个单位得到P,推出点D向左平移1个单位,向上平移
个单位得到P,推出点D向左平移1个单位,向上平移![]() 个单位得到Q,再根据对称性可得Q′、Q″的坐标.
个单位得到Q,再根据对称性可得Q′、Q″的坐标.
(1)∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
(2)∵直线AB与x轴,y轴交于![]() 、
、![]() 两点
两点
∴直线AB的解析式为![]()
∵![]() ,
,
∴![]() ,设
,设![]() ,则
,则![]()
把![]() 代入
代入![]() 得到
得到![]() ,
,
∴![]()
∵![]() ,
,![]()
∴直线BC的解析式为![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,把
,把![]() 代入得到
代入得到![]()
∴直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() ,
,
∴![]()
∴![]() 平移的距离是
平移的距离是![]() 个单位.
个单位.
(3)如图3中,作CP∥AB交y轴于P,作PQ∥CD交AB于Q,则四边形PCDQ是平行四边形,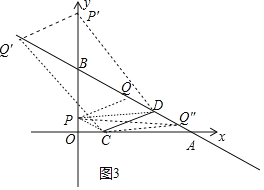
易知直线PC的解析式为y=-![]() x+
x+![]() ,
,
∴P(0,![]() ),
),
∵点C向左平移1个单位,向上平移![]() 个单位得到P,
个单位得到P,
∴点D向左平移1个单位,向上平移![]() 个单位得到Q,
个单位得到Q,
∴Q(2,![]() ),
),
当CD为对角线时,四边形PCQ″D是平行四边形,可得Q″![]() ,
,
当四边形CDP′Q′为平行四边形时,可得Q′![]() ,
,
综上所述, 存在满足条件的点Q,其坐标为![]() 或
或![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.

(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一项工程,甲队单独做需40天完成,若乙队先做30天后,甲、乙两队一起合做20天恰好完成任务,请问:
(1)乙队单独做需要多少天才能完成任务?
(2)现将该工程分成两部分,甲队做其中一部分工程用了x天,乙队做另一部分工程用了y天,若x; y都是正整数,且甲队做的时间不到15天,乙队做的时间不到70天,那么两队实际各做了多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点
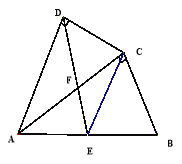
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求
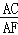 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠AOB=90°,点C、D分别在射线OA、OB上,点E在∠AOB内部.
(1)根据语句画图形:
①画直线CE;
②画射线OE;
③画线段DE,
(2)结合图形,完成下面的填空:
①与∠ODE互补的角是 ;
②若∠BOE =
 ∠AOE,则∠BOE的大小是 .
∠AOE,则∠BOE的大小是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表,根据相关信息完成下列问题:
(1)统计表中的
 ,
, ;
;(2)扇形统计图中“C组”所对应的圆心角的度数是 ;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.

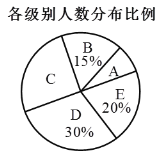
-
科目: 来源: 题型:
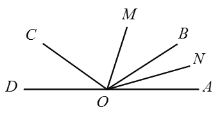
查看答案和解析>>【题目】如图,已知O为直线AD上一点,∠AOC与∠AOB互补,OM和ON分别是∠AOC和∠AOB的平分线.
(1) 试说明:∠AOB=∠COD;
(2) 若∠COD=36°,求∠MON的度数.
相关试题

