【题目】如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为

A. ![]() B. 2
B. 2![]() C.
C. ![]() D. 3
D. 3![]()
参考答案:
【答案】C
【解析】由已知可知△ADC是等腰直角三角形,根据斜边AC=8可得AD=4![]() ,在Rt△ABD中,由∠B=60°,可得BD=
,在Rt△ABD中,由∠B=60°,可得BD=![]() =
=![]() ,再由BE平分∠ABC,可得∠EBD=30°,从而可求得DE长,再根据AE=AD-DE即可
,再由BE平分∠ABC,可得∠EBD=30°,从而可求得DE长,再根据AE=AD-DE即可
∵AD⊥BC,
∴△ADC是直角三角形,
∵∠C=45°,
∴∠DAC=45°,
∴AD=DC,
∵AC=8,
∴AD=4![]() ,
,
在Rt△ABD中,∠B=60°,∴BD=![]() =
=![]() =
=![]() ,
,
∵BE平分∠ABC,∴∠EBD=30°,
∴DE=BDtan30°=![]() =
=![]() ,
,
∴AE=AD-DE=![]() ,
,
故选C.
-
科目: 来源: 题型:
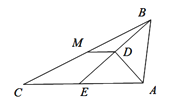
查看答案和解析>>【题目】如图,在△ABC中,点E是边AC上一点,线段BE垂直于∠BAC的平分线于点D,点M为边BC的中点,连接DM.
(1)求证: DM=
 CE;
CE; (2)若AD=6,BD=8,DM=2,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明为了解政府调整水价方案的社会反响,随机访问了自己居住小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1、图2.

小明发现每月每户的用水量为5
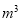 -35
-35 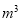 之间,有8户居民对用水价格调价涨幅抱无所谓,不会考虑用水方式的改变.根据小明绘制的图表和发现的信息,完成下列问题:
之间,有8户居民对用水价格调价涨幅抱无所谓,不会考虑用水方式的改变.根据小明绘制的图表和发现的信息,完成下列问题:(1)
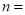 ,小明调查了 户居民,并补全图1;
,小明调查了 户居民,并补全图1;(2)每月每户用水量的中位数和众数分别落在什么范围?
(3)如果小明所在小区有1800户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2-2(m-1)x-m(m+2)=0
(1) 求证:此方程总有两个不相等的实数根
(2) 若x=-2是此方程的一个根,求实数m的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程.
(1)

(2)
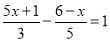
(3)
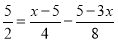
(4)
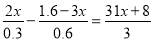
-
科目: 来源: 题型:
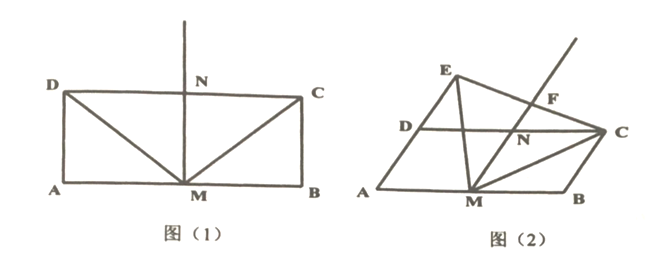
查看答案和解析>>【题目】如图(1),在矩形
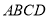 中,
中,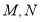 分别是
分别是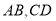 的中点,作射线
的中点,作射线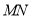 ,连接
,连接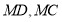 .
.
(1)请直接写出线段
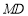 与
与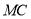 的数量关系;
的数量关系;(2)将矩形
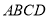 变为平行四边形,其中
变为平行四边形,其中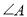 为锐角,如图(2),
为锐角,如图(2),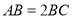 ,
,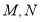 分别是
分别是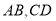 的中点,过点
的中点,过点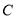 作
作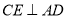 交射线
交射线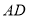 于点
于点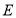 ,交射线
,交射线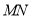 于点
于点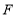 ,连接
,连接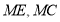 ,求证:
,求证: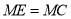 ;
;(3)写出
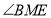 与
与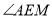 的数量关系,并证明你的结论.
的数量关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】若直线l1经过点(0,4),l2经过(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为
A. (-2,0) B. (2,0) C. (-6,0) D. (6,0)
相关试题

