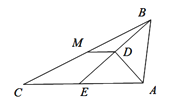
【题目】如图,在△ABC中,点E是边AC上一点,线段BE垂直于∠BAC的平分线于点D,点M为边BC的中点,连接DM.
(1)求证: DM=![]() CE;
CE;
(2)若AD=6,BD=8,DM=2,求AC的长.
参考答案:
【答案】(1)见解析 (2)AC=14
【解析】
(1)证△BAD≌△EAD,推出AB=AE,BD=DE,根据三角形的中位线性质得出DM=![]() CE即可;
CE即可;
(2)根据勾股定理求出AB,求出AE,根据三角形的中位线求出CE,即可得出答案.
∵AD⊥BE,
∴∠ADB=∠ADE=90°,
∵AD为∠BAC的平分线,
∴∠BAD=∠EAD,
在△BAD和△EAD中,
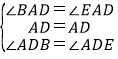 ,
,
∴△BAD≌△EAD(SAS),
∴AB=AE,BD=DE,
∵M为BC的中点,
∴DM=![]() CE
CE
(2)∵在Rt△ADB中,∠ADB=90°,AD=6,BD=8,
∴由勾股定理得:AE=AB=![]() ,
,
∵DM=2,DM=![]() CE,
CE,
∴CE=4,
∴AC=10+4=14.
-
科目: 来源: 题型:
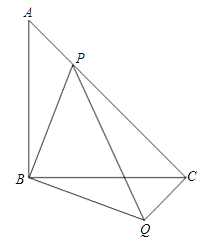
查看答案和解析>>【题目】如图,等腰直角△ABC中,∠ABC=90°,点P在AC上,将△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ.
(1)求∠PCQ的度数;
(2)当AB=4,AP:PC=1:3时,求PQ的大小;
(3)当点P在线段AC上运动时(P不与A重合),请写出一个反映PA2,PC2,PB2之间关系的等式,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】说明理由
如图,∠1+∠2=230°,b∥c, 则∠1、∠2、∠3、∠4各是多少度?
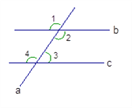
解:∵ ∠1=∠2 (_________________________)
∠1+∠2=230°
∴∠1 =∠2 =________(填度数)
∵ b∥c
∴∠4 =∠2= ________(填度数)
( )
∠2 +∠3 =180° ( )
∴∠3 =180°-∠2 =_________(填度数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是

A.4 B.3 C.2 D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 分别平分
分别平分 和
和 ,交
,交 于点
于点 ,线段
,线段 相交于点M.
相交于点M.(1)求证:
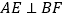 ;
;(2)若
 ,则
,则 的值是__________.
的值是__________. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
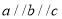 ,
,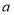 与
与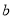 之间的距离为3,
之间的距离为3, 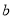 与
与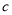 之间的距离为6,
之间的距离为6, 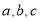 分别等边三角形
分别等边三角形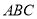 的三个顶点,则此三角形的边长为__________.
的三个顶点,则此三角形的边长为__________.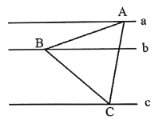
-
科目: 来源: 题型:
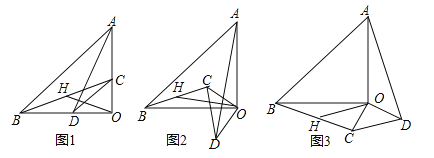
查看答案和解析>>【题目】(2017黑龙江省龙东地区)已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°.连接AD,BC,点H为BC中点,连接OH.
(1)如图1所示,易证:OH=
 AD且OH⊥AD(不需证明)
AD且OH⊥AD(不需证明)(2)将△COD绕点O旋转到图2,图3所示位置时,线段OH与AD又有怎样的关系,并选择一个图形证明你的结论.
相关试题

