【题目】如图(1),在矩形![]() 中,
中,![]() 分别是
分别是![]() 的中点,作射线
的中点,作射线![]() ,连接
,连接![]() .
.
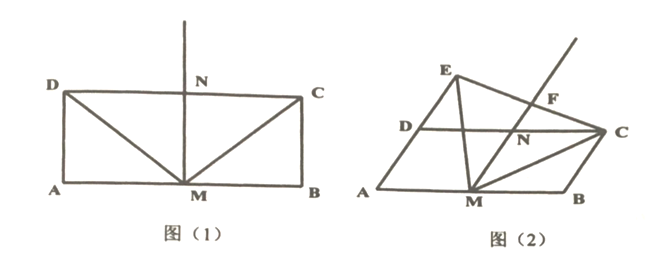
(1)请直接写出线段![]() 与
与![]() 的数量关系;
的数量关系;
(2)将矩形![]() 变为平行四边形,其中
变为平行四边形,其中![]() 为锐角,如图(2),
为锐角,如图(2),![]() ,
,![]() 分别是
分别是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)写出![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
参考答案:
【答案】(1)MD=MC;(2)见解析;(3)∠BME=3∠AEM,证明见解析.
【解析】
(1)由“SAS”可证△ADM≌△BCM,可得MD=MC;
(2)由题意可证四边形ADNM是平行四边形,可得AD∥MN,可得EF=FC,MF⊥EC,由线段垂直平分线的性质可得ME=MC;
(3)由等腰三角形的性质和平行线的性质可得∠BME=3∠AEM.
解:(1)∵四边形ABCD是矩形,
∴AD=BC,∠A=∠B=90°,
∵点M是AB中点,
∴AM=BM,
∴△ADM≌△BCM(SAS),
∴MD=MC;
(2)∵M、N分别是AB、CD的中点,
∴AM=BM,CN=DN,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴DN=AM=CN=BM,
∴四边形ADNM是平行四边形,
∴AD∥MN,
∴![]() ,∠AEC=∠NFC=90°,
,∠AEC=∠NFC=90°,
∴EF=CF,且MF⊥EC,
∴ME=MC;
(3)∠BME=3∠AEM,
证明:∵EM=MC,EF=FC,
∴∠EMF=∠FMC,
∵AB=2BC,M是AB中点,
∴MB=BC,
∴∠BMC=∠BCM,
∵MN∥AD,AD∥BC,
∴AD∥MN∥BC,
∴∠AEM=∠EMF,∠FMC=∠BCM,
∴∠AEM=∠EMF=∠FMC=∠BCM=∠BMC,
∴∠BME=3∠AEM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2-2(m-1)x-m(m+2)=0
(1) 求证:此方程总有两个不相等的实数根
(2) 若x=-2是此方程的一个根,求实数m的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为

A.
 B. 2
B. 2 C.
C.  D. 3
D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程.
(1)

(2)
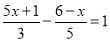
(3)
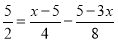
(4)
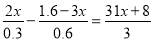
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线l1经过点(0,4),l2经过(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为
A. (-2,0) B. (2,0) C. (-6,0) D. (6,0)
-
科目: 来源: 题型:
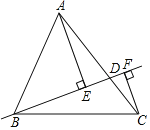
查看答案和解析>>【题目】如图,在△ABC中,AB=13,BC=14,AC=15,点D在AC上(可与点A,C重合),分别过点A、C作直线BD的垂线,垂足为E,F,则AE+CF的最大值为_____,最小值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在Rt△ABC=90
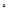 ,如果CD、CM分别是斜边上的高和中线,AC=2,BC=4,那么下列结论中错误的是( )
,如果CD、CM分别是斜边上的高和中线,AC=2,BC=4,那么下列结论中错误的是( )
A. ∠ACD=∠BB. CM=
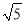 C. ∠B=30
C. ∠B=30 D. CD=
D. CD=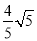
相关试题

