【题目】某汽车销售公司经销某品牌 A 款汽车,随着汽车的普及,其价格也在不断下降, 今年5月份 A 款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的 A 款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份 A 款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的 B 款汽车,已知 A 款汽车每辆进价为7.5万元,B 款汽车每辆进价为 6 万元,公司预计用不多余105 万元且不少于99 万元的资金购买这两款汽车共15辆,有几种进货方案?
(3)在(2)的前提下,如果 B 款汽车每辆售价为8 万元,为打开 B 款汽车的销路,公司决定每售出一辆 B 款汽车,返还顾客现金 a 万元0 a 2,此时,哪种方案对公司更有利?最大利润是多少?
参考答案:
【答案】(1)今年5月份A款汽车每辆售价9万元;(2)共有5种进货方案;(3)见详解
【解析】
(1)求单价应根据数量来列等量关系.等量关系为:今年的销售数量=去年的销售数量.
(2)关系式为:99≤A款汽车总价+B款汽车总价≤105.
(3)列出利润W的关系式,根据a的大小,分情况讨论.
解:(1)设今年5月份A款汽车每辆售价m万元.则:![]() ,
,
解得:m=9.
经检验,m=9是原方程的根,符合题意.
答:今年5月份A款汽车每辆售价9万元;
(2)设购进A款汽车x辆.则:![]()
解得:6≤x≤10.
∵x的正整数解为6,7,8,9,10,
∴共有5种进货方案;
(3)设总获利为W万元,购进A款汽车x辆,则:![]()
=![]()
①当a =0.5时,(2)中所有方案获利相同,利润为22.5万元
由于要打开 B 款汽车的销路,因此购买A款汽车6辆,B款汽车9辆对公司有利.
②当0<a<0.5时,W随x的增大而减小,
∴当x=6时, W=![]()
利润最大为27-9a,因此购买A款汽车6辆,B款汽车9辆对公司有利.
③当0.5<a<2时,W随x的增大而增大,
∴当x=10时,W=![]()
利润最大为25-5a,因此购买A款汽车10辆,B款汽车5辆对公司有利.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知A.B是直线上的两点,且AB=6,若P在这条直线上,且PA=5.
①画出P点在直线AB上的大致位置图;
②求PB长.
(2)尺规作图(不写作法.保留作图痕迹)
已知线段
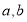 ,求作:线段MN,使MN=
,求作:线段MN,使MN=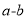 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF.
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
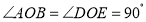 ,OC是BO的延长线,OF平分∠AOD,∠AOE=35.
,OC是BO的延长线,OF平分∠AOD,∠AOE=35.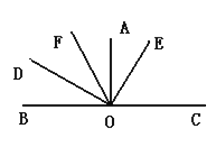
(1)求∠EOC的度数;
(2)求∠BOF的度数;
(3)请你写出图中三对相等的角.
-
科目: 来源: 题型:
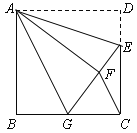
查看答案和解析>>【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
(1)求证:①△ABG≌△AFG; ②BG=GC;
(2)求△FGC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c为非零的实数,则
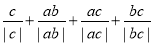 的最大值与最小值的差为________.
的最大值与最小值的差为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:①已知A(x1,y1)、B(x2,y2),则AB=
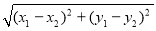 ;② 已知A(x0,y0)直线 l 的方程为 Ax By C 0, 则 A 到直线的距离
;② 已知A(x0,y0)直线 l 的方程为 Ax By C 0, 则 A 到直线的距离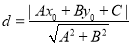
(1)已知 A2,5、 B1,1,求 AB ;
(2)已知 A2,1,直线l : 3x 4y 5 0,求 A 到直线的距离;
(3)求两平行直线3x 4y1 0与3x 4 y 8 0之间的距离;
(4)求
 的最小值.
的最小值.
相关试题

