【题目】定义:①已知A(x1,y1)、B(x2,y2),则AB=![]() ;② 已知A(x0,y0)直线 l 的方程为 Ax By C 0, 则 A 到直线的距离
;② 已知A(x0,y0)直线 l 的方程为 Ax By C 0, 则 A 到直线的距离![]()
(1)已知 A2,5、 B1,1,求 AB ;
(2)已知 A2,1,直线l : 3x 4y 5 0,求 A 到直线的距离;
(3)求两平行直线3x 4y1 0与3x 4 y 8 0之间的距离;
(4)求![]() 的最小值.
的最小值.
参考答案:
【答案】(1)5;(2)3;(3)![]() ;(4)
;(4)![]()
【解析】
(1)由A与B的坐标,利用题中的方法求出AB的长即可;
(2)利用点到直线的距离公式求出A到直线的距离即可;
(3)从直线3x 4y1 0上找一个点,求出该点到3x 4 y 8 0的距离,即为两条平行线的距离;
(4)先将![]() 转化成两点间距离公式
转化成两点间距离公式![]() 形式,把原式最小值转化为两点间距离问题.
形式,把原式最小值转化为两点间距离问题.
解:(1)将A2,5、 B1,1,代入AB=![]()
得:AB=![]()
所以AB长为5;
(2)将A2,1,直线l : 3x 4y 5 0,代入![]()
可得:![]() ,
,
所以A 到直线的距离为3;
(3)在直线3x 4y1 0上取x=1,则y=-1,
∴(1,-1)在直线3x 4y1 0上,
将(1,-1)和3x 4 y 8 0代入![]()
可得:![]()
所以两平行直线3x 4y1 0与3x 4 y 8 0之间的距离为![]() ;
;
(4)![]()
![]()
![]()
所以原式的值即为点(x,0)到点(-2,-1)和点(3,4)的距离和,
由于点(-2,-1)和点(3,4)位于点(x,0)两侧,
那么原式的最小值即为点(-2,-1)和点(3,4)两点间的距离,
∵![]()
![]() ,
,
∴![]() 的最小值为
的最小值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车销售公司经销某品牌 A 款汽车,随着汽车的普及,其价格也在不断下降, 今年5月份 A 款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的 A 款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份 A 款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的 B 款汽车,已知 A 款汽车每辆进价为7.5万元,B 款汽车每辆进价为 6 万元,公司预计用不多余105 万元且不少于99 万元的资金购买这两款汽车共15辆,有几种进货方案?
(3)在(2)的前提下,如果 B 款汽车每辆售价为8 万元,为打开 B 款汽车的销路,公司决定每售出一辆 B 款汽车,返还顾客现金 a 万元0 a 2,此时,哪种方案对公司更有利?最大利润是多少?
-
科目: 来源: 题型:
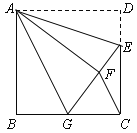
查看答案和解析>>【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
(1)求证:①△ABG≌△AFG; ②BG=GC;
(2)求△FGC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c为非零的实数,则
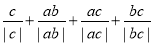 的最大值与最小值的差为________.
的最大值与最小值的差为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数
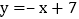 与正比例函数
与正比例函数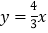 的图象交于点
的图象交于点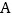 ,且与
,且与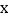 轴交于点
轴交于点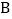 .
.(1)直接写出点
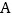 的坐标为 ;点
的坐标为 ;点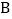 的坐标为 ;
的坐标为 ;(2)过点
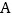 作
作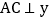 轴于点
轴于点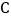 ,过点
,过点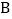 作直线l∥y轴.动点
作直线l∥y轴.动点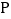 从点
从点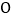 出发,以每秒
出发,以每秒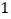 个单位长的速度,沿
个单位长的速度,沿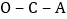 的路线向点
的路线向点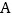 运动;同时直线
运动;同时直线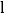 从点
从点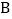 出发,以相同速度向左平移,在平移过程中,直线
出发,以相同速度向左平移,在平移过程中,直线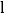 交
交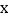 轴于点
轴于点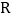 ,交线段
,交线段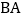 或线段
或线段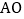 于点
于点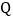 .当点
.当点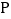 到达点
到达点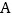 时,点
时,点 和直线
和直线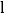 都停止运动.在运动过程中,设动点
都停止运动.在运动过程中,设动点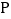 运动的时间为
运动的时间为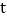 秒.
秒. 当
当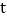 为何值时,以
为何值时,以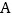 、
、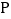 、
、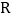 为顶点的三角形的面积为
为顶点的三角形的面积为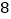 ;
; 是否存在以
是否存在以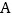 、
、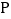 、
、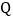 为顶点的三角形是等腰三角形?若存在,直接写出
为顶点的三角形是等腰三角形?若存在,直接写出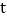 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.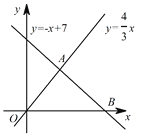
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
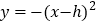 (
(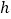 为常数),当自变量
为常数),当自变量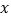 的值满足
的值满足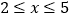 时,与其对应的函数值
时,与其对应的函数值 的最大值为-1,则
的最大值为-1,则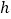 的值为( )
的值为( )A. 3或6 B. 1或6 C. 1或3 D. 4或6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 的边长为1,点
的边长为1,点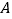 与原点重合,点
与原点重合,点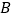 在
在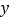 轴的正半轴上,点
轴的正半轴上,点 在
在 轴的负半轴上将正方形
轴的负半轴上将正方形 绕点
绕点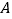 逆时针旋转
逆时针旋转 至正方形
至正方形 的位置,
的位置,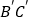 与
与 相交于点
相交于点 ,则
,则 的坐标为____________.
的坐标为____________.
相关试题

