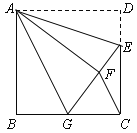
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
(1)求证:①△ABG≌△AFG; ②BG=GC;
(2)求△FGC的面积.
参考答案:
【答案】(1)①见解析,②见解析;(2)![]()
【解析】
(1)①根据折叠的性质可得∠B=∠AFG=90,AB=AF,AG=AG,根据HL定理即可证两三角形全等;②设BG=FG=x,(x>0),则CG=6-x,EG=2+x,在Rt△CEG中,利用勾股定理即可列方程求解;(2)根据三角形的面积公式可得:S△FGC=![]() S△EGC,即可求解.
S△EGC,即可求解.
(1)证明:
①在正方形ABCD中,AD=AB,∠D=∠B=∠C=90
又∵△ADE沿AE对折至△AFE,延长EF交边BC于点G
∴∠AFG=∠AFE=∠D=90,AF=AD,
即有∠B=∠AFG=90,AB=AF,AG=AG,
∴△ABG≌△AFG
②∵AB=6,点E在边CD上,且CD=3DE,∴DE=FE=2,CE=4
不妨设BG=FG=x,(x>0),则CG=6-x,EG=2+x,
在Rt△CEG中,(2+x)2=42+(6-x)2
解得x=3,于是BG=GC=3
(2)∵![]() ,∴
,∴![]()
∴S△FGC=![]() S△EGC=
S△EGC=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.
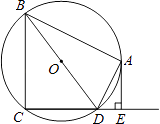
(1)求证:AE是⊙O的切线;
(2)如果AB=4,AE=2,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)、求证:四边形AODE是矩形;(2)、若AB=6,∠BCD=120°,求四边形AODE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称
单价(元)
数量(个)
金额(元)
挂钟
30
2
60
垃圾桶
15
塑料鞋架
40
艺术字画
a
2
90
电热水壶
35
1
b
合计
8
280
(1)直接写出a= , b=;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术字画和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】某种事物经历了加热,冷却两个联系过程,折线图DEF表示食物的温度y(℃)与时间x(s)之间的函数关系(0≤x≤160),已知线段EF表示的函数关系中,时间每增加1s,食物温度下降0.3℃,根据图象解答下列问题;
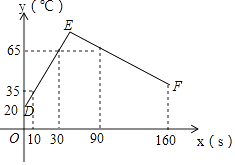
(1)当时间为20s、100s时,该食物的温度分别为℃,℃;
(2)求线段DE所表示的y与x之间的函数表达式;
(3)时间是多少时,该食物的温度最高?最高是多少? -
科目: 来源: 题型:
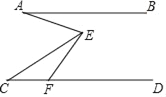
查看答案和解析>>【题目】如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,矩形OABC的对角线AC=12,∠ACO=30°
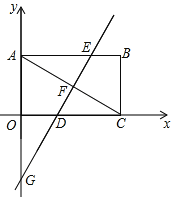
(1)求B、C两点的坐标;
(2)过点G(
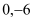 )作GF⊥AC,垂足为F,直线GF分别交AB、OC于点E、D,求直线DE的解析式;
)作GF⊥AC,垂足为F,直线GF分别交AB、OC于点E、D,求直线DE的解析式;(3)在⑵的条件下,若点M在直线DE上,平面内是否存在点P,使以O、F、M、P为顶点的四边形是菱形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
相关试题

