Question

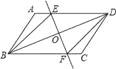
【题目】已知：如图，在平行四边形ABCD中，O为对角线BD的中点，过点O的直线EF分别交AD，BC于E，F两点，连结BE，DF．

（1）求证：△DOE≌△BOF．

（2）当∠DOE等于多少度时，四边形BFDE为菱形？请说明理由．

Answer 1

【答案】（1）证明见解析；（2）当∠DOE=90°时，四边形BFED为菱形，理由见解析.

【解析】试题分析：（1）利用平行四边形的性质以及全等三角形的判定方法得出△DOE≌△BOF（ASA）；

（2）首先利用一组对边平行且相等的四边形是平行四边形得出四边形EBFD是平行四边形，进而利用垂直平分线的性质得出BE=ED，即可得出答案．

试题解析：（1）∵在ABCD中，O为对角线BD的中点，

∴BO=DO，∠EDB=∠FBO，

在△EOD和△FOB中

，

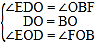∴△DOE≌△BOF（ASA）；

（2）当∠DOE=90°时，四边形BFDE为菱形，

理由：∵△DOE≌△BOF，∴OE=OF，又∵OB=OD，∴四边形EBFD是平行四边形，

∵∠EOD=90°，∴EF⊥BD，∴四边形BFDE为菱形．