Question

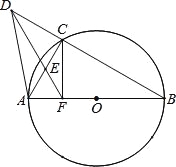
【题目】已知AB是半径为1的圆O直径，C是圆上一点，D是BC延长线上一点，过点D的直线交AC于E点，且△AEF为等边三角形

（1）求证：△DFB是等腰三角形；

（2）若DA=AF，求证：CF⊥AB．

Answer 1

【答案】（1）证明详见解析；（2）证明详见解析.

【解析】

试题分析：（1）由AB是⊙O直径，得到∠ACB=90°，由于△AEF为等边三角形，得到∠CAB=∠EFA=60°，根据三角形的外角的性质即可得到结论；

（2）过点A作AM⊥DF于点M，设AF=2a，根据等边三角形的性质得到FM=EM=a，AM=a，在根据已知条件得到AB=AF+BF=8a，根据直角三角形的性质得到AE=EF=AF=CE=2a，推出∠ECF=∠EFC，根据三角形的内角和即可得到结论．

试题解析：（1）∵AB是⊙O直径，

∴∠ACB=90°，

∵△AEF为等边三角形，

∴∠CAB=∠EFA=60°，

∴∠B=30°，

∵∠EFA=∠B+∠FDB，

∴∠B=∠FDB=30°，

∴△DFB是等腰三角形；

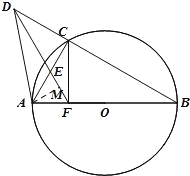
（2）过点A作AM⊥DF于点M，设AF=2a，

∵△AEF是等边三角形，∴FM=EM=a，AM=a，

在Rt△DAM中，AD=AF=a，AM=a，

∴DM=5a，∴DF=BF=6a，

∴AB=AF+BF=8a，

在Rt△ABC中，∠B=30°，∠ACB=90°，∴AC=4a，

∵AE=EF=AF=2a，

∴CE=AC﹣AE=2a，

∴∠ECF=∠EFC，

∵∠AEF=∠ECF+∠EFC=60°，∴∠CFE=30°，

∴∠AFC=∠AFE+∠EFC=60°+30°=90°，

∴CF⊥AB．