【题目】如图,以ABCD 的四条边为边,分别向外作正方形,连结 EF,GH,IJ,KL.如果ABCD 的 面积为 8,则图中阴影部分四个三角形的面积和为( )

A.8B.12C.16D.20
参考答案:
【答案】C
【解析】
连接AC,通过证明△EAF≌△ABC,可求S△EAF=![]() =4,同理求出理S△BHG= S△CIJ= S△DLK=
=4,同理求出理S△BHG= S△CIJ= S△DLK=![]() =4,即可求出阴影部分四个三角形的面积和.
=4,即可求出阴影部分四个三角形的面积和.
解:连接AC,
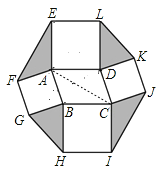
∵四边形ABGF和四边形ADLE是正方形,
∴AE=AD,AF=AB,∠FAB=∠EAD=90°,
∴∠EAF+∠BAD=360°-90°-90°=180°,
∵∠BAD+∠ABC=180°,
∴∠EAF=∠ABC,
在△EAF和△ABC中,
∵AE=AD=BC,
∠EAF=∠ABC,
AF=AB,
∴△EAF≌△ABC,
∴S△EAF≌S△ABC=![]() =4,
=4,
同理可求:S△BHG= S△CIJ= S△DLK=![]() =4,
=4,
∴阴影部分的面积S=S△AEF+S△BGH+S△CIJ+S△DLK=4×4=16.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,已知点A(0,10),点B(m,10)在第一象限,连接AB、OB.
(1)如图1,若OB=12,求m的值.

(2)如图2,当m=10时,过B作BC⊥x轴于C,E为AB边上一点,AE=
 ,把△OAE沿直线OE翻折得到△OFE(点A的对应点为点F),连接BF、CF,求证:BF⊥CF.
,把△OAE沿直线OE翻折得到△OFE(点A的对应点为点F),连接BF、CF,求证:BF⊥CF.
(3)如图3,将△AOB沿直线OB翻折得到△GOB(点A的对应点为点G),若点G到x轴的距离不大于8,直接写出m的取值范围为 .

-
科目: 来源: 题型:
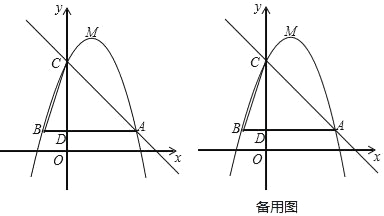
查看答案和解析>>【题目】如图,已知二次函数y=﹣x2+bx+c(其中b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(1)求该二次函数的解析式及点M的坐标.
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围.
(3)沿直线AC方向平移该二次函数图象,使得CM与平移前的CB相等,求平移后点M的坐标.
(4)点P是直线AC上的动点,过点P作直线AC的垂线PQ,记点M关于直线PQ的对称点为M′.当以点P、A、M、M′为顶点的四边形为平行四边形时,直接写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在给定的一张平行四边形纸片上按如下操作:连结AC,作AC的垂直平分线MN分别交AD、AC、BC于M、O、N,连结AN,CM,则四边形ANCM是( )

A. 矩形 B. 菱形 C. 正方形 D. 无法判断
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,边长为a,点O是对角线AC的中点,点E是BC边上的一个动点,OE⊥OF交AB边于点F,点G,H分别是点E,F关于直线AC的对称点,点E从点C运动到点B时,则图中阴影部分的面积是___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要使平行四边形ABCD成为菱形,需添加的条件是( )

A. AC=BD B. ∠1=∠2 C. ∠ABC=90° D. ∠1=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市防洪大堤的横截面如图所示,已知AE∥BC,背水坡AB的坡度
 ,且AB=26米.身高1.8米的小明竖直站立于A点,眼睛在M点处测得竖立的高压电线杆顶端D点的仰角为24°,已知地面CB宽30米,则高压电线杆CD的高度约为( )(结果精确到整数,参考数据:sin24°≈0.40,cos24°≈0.91,tan24°≈0.45)
,且AB=26米.身高1.8米的小明竖直站立于A点,眼睛在M点处测得竖立的高压电线杆顶端D点的仰角为24°,已知地面CB宽30米,则高压电线杆CD的高度约为( )(结果精确到整数,参考数据:sin24°≈0.40,cos24°≈0.91,tan24°≈0.45)
A. 33米 B. 34米 C. 35米 D. 36米
相关试题

