搜索
【题目】如图，在给定的一张平行四边形纸片上按如下操作：连结AC，作AC的垂直平分线MN分别交AD、AC、BC于M、O、N，连结AN，CM，则四边形ANCM是（ ）
A. 矩形 B. 菱形 C. 正方形 D. 无法判断
参考答案：
【答案】B
【解析】
首先证明△AOM≌△CON（ASA），可得MO=NO，再根据对角线互相平分的四边形是平行四边形可判定判定四边形ANCM是平行四边形，再由AC⊥MN，可根据对角线互相垂直的四边形是菱形判定出ANCM是菱形.
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠DAC=∠ACN，
∵MN是AC的垂直平分线，
∴AO=CO，
在△AOM和△CON中
，
∴△AOM≌△CON（ASA），
∴MO=NO，
∴四边形ANCM是平行四边形，
∵AC⊥MN，
∴四边形ANCM是菱形，
故选B.
-
科目： 来源： 题型：
查看答案和解析>>【题目】2019年是中国建国70周年，作为新时期的青少年，我们应该肩负起实现粗国伟大复兴的责任，为了培养学生的爱国主义情怀，我校学生和老师在5月下旬集体乘车去抗日战争纪念馆研学，已知学生的人数是老师人数的12倍多20人，学生和老师总人数有540人．
（1）请求出去抗日战争纪念馆研学的学生和老师的人数各是多少？
（2）如果学校准备租赁A型车和B型车共14辆（其中B型车最多7辆），已知A型车每车最多可以载35人，日租金为2000元，B型车每车最多可以载45人，日租金为3000元，请求出最经济的租车方案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平面直角坐标系中，已知点A（0，10），点B（m，10）在第一象限，连接AB、OB．
（1）如图1，若OB=12，求m的值．
（2）如图2，当m=10时，过B作BC⊥x轴于C，E为AB边上一点，AE=
，把△OAE沿直线OE翻折得到△OFE（点A的对应点为点F），连接BF、CF，求证：BF⊥CF．
（3）如图3，将△AOB沿直线OB翻折得到△GOB（点A的对应点为点G），若点G到x轴的距离不大于8，直接写出m的取值范围为 ．
-
科目： 来源： 题型：
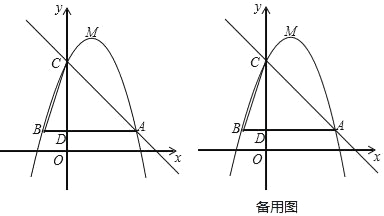
查看答案和解析>>【题目】如图，已知二次函数y=﹣x2+bx+c（其中b，c为常数）的图象经过点A（3，1），点C（0，4），顶点为点M，过点A作AB∥x轴，交y轴于点D，交该二次函数图象于点B，连结BC．
（1）求该二次函数的解析式及点M的坐标．
（2）若将该二次函数图象向下平移m（m＞0）个单位，使平移后得到的二次函数图象的顶点落在△ABC的内部（不包括△ABC的边界），求m的取值范围．
（3）沿直线AC方向平移该二次函数图象，使得CM与平移前的CB相等，求平移后点M的坐标．
（4）点P是直线AC上的动点，过点P作直线AC的垂线PQ，记点M关于直线PQ的对称点为M′．当以点P、A、M、M′为顶点的四边形为平行四边形时，直接写出点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以ABCD 的四条边为边，分别向外作正方形，连结 EF，GH，IJ，KL．如果ABCD 的 面积为 8，则图中阴影部分四个三角形的面积和为（ ）
A.8B.12C.16D.20
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，边长为a，点O是对角线AC的中点，点E是BC边上的一个动点，OE⊥OF交AB边于点F，点G，H分别是点E，F关于直线AC的对称点，点E从点C运动到点B时，则图中阴影部分的面积是___________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，要使平行四边形ABCD成为菱形，需添加的条件是（ ）
A. AC=BD B. ∠1=∠2 C. ∠ABC=90° D. ∠1=90°
相关试题
