【题目】端午节,在大明湖举行第七届会民健身运动会龙舟比赛中,甲、乙两队在500米的赛道上,所划行的路程y(m)与时间x(min)之间的函数关系如图所示,下列说法,其中正确的有( )

①乙队比甲队提前0.25min到达终点;
②0.5min后,乙队比甲队每分钟快40m;
③当乙队划行110m时,此时落后甲队15m;
④自1.5min开始,甲队若要与乙队同时到达终点,甲队的速度需要提高到260m/min.
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】
观察函数图象可知,函数的横坐标表示时间,纵坐标表示路程,根据图象上特殊点的意义即可求出答案.
①由横坐标看出乙队比甲队提前0.25min到达终点,此结论正确;
②乙AB段的解析式为y=240x﹣40,乙的速度是240m/min;甲的解析式为y=200x,甲的速
度是200m/min,0.5min后,乙队比甲队每分钟快40m,此结论正确;
③乙AB段的解析式为y=240x﹣40,当y=110时,![]() 甲的解析式为y=200x,当
甲的解析式为y=200x,当![]()
时,y=125,当乙队划行110m时,此时落后甲队15m,此结论正确;
④甲的解析式为y=200x,当x=1.5时,y=300,甲乙同时到达(500﹣300)÷(2.25﹣1.5)
≈267m/min,此结论错误;
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B两点,(点A在点B的左侧),与直线AC交于点C(2,3),直线AC与抛物线的对称轴l相交于点D,连接BD.

(1)求抛物线的函数表达式,并求出点D的坐标;
(2)如图2,若点M、N同时从点D出发,均以每秒1个单位长度的速度分别沿DA、DB运动,连接MN,将△DMN沿MN翻折,得到△D′MN,判断四边形DMD′N的形状,并说明理由,当运动时间t为何值时,点D′恰好落在x轴上?
(3)在平面内,是否存在点P(异于A点),使得以P、B、D为顶点的三角形与△ABD相似(全等除外)?若存在,请直接写出点P的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在⊙O的直径AB上,AB=6,AC=1.点P为⊙O上的任意一点,当∠OPC取最大值时,则△OCP的面积为 .
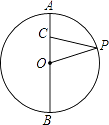
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果10b=n,那么称b为n的劳格数,记为b= d(n).
(1)根据劳格数的定义,可知d(10)=1,d(102)=2,直接写出 d(103)的值.
(2)劳格数有如下运算性质:若m,n为正数,则d(mn)= d(m)+ d(n);d(
 )= d(m)- d(n).
)= d(m)- d(n).根据运算性质,求:
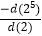 ,若
,若 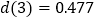 ,直接写出
,直接写出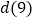 ,
,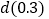 的值.
的值.(3)下表中与数x对应的劳格数
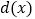 有且只有两个是错误的,请找出错误的劳格数并改正.
有且只有两个是错误的,请找出错误的劳格数并改正. 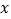
1.5
3
5
6
8
9
12
27
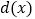
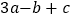
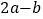
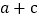

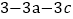
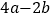
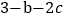
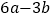
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=
 (k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 . 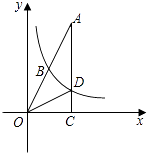
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知当x1=a,x2=b,x3=c时,二次函数y=
 x2+mx对应的函数值分别为y1 , y2 , y3 , 若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3 , 则实数m的取值范围是 .
x2+mx对应的函数值分别为y1 , y2 , y3 , 若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3 , 则实数m的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第
 个图中正方形和等边三角形的个数之和为 个.
个图中正方形和等边三角形的个数之和为 个. 
相关试题

