【题目】如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B两点,(点A在点B的左侧),与直线AC交于点C(2,3),直线AC与抛物线的对称轴l相交于点D,连接BD.
(1)求抛物线的函数表达式,并求出点D的坐标;
(2)如图2,若点M、N同时从点D出发,均以每秒1个单位长度的速度分别沿DA、DB运动,连接MN,将△DMN沿MN翻折,得到△D′MN,判断四边形DMD′N的形状,并说明理由,当运动时间t为何值时,点D′恰好落在x轴上?
(3)在平面内,是否存在点P(异于A点),使得以P、B、D为顶点的三角形与△ABD相似(全等除外)?若存在,请直接写出点P的坐标,若不存在,请说明理由.
参考答案:
【答案】
(1)
解:将点A(﹣1,0)、C(2,3)代入y=﹣x2+bx+c,得:
![]() ,
,
解得: ![]() ,
,
∴抛物线的解析式为y=﹣x2+2x+3,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴抛物线的对称轴为直线x=1,
设直线AC的函数解析式为y=kx+b,
将A(﹣1,0)、C(2,3)代入y=kx+b,得:
![]() ,
,
解得: ![]() ,
,
∴直线AC的函数解析式为y=x+1,
又∵点D是直线AC与抛物线的对称轴的交点,
∴xD=1,yD=1+1=2,
∴点D的坐标为(1,2)
(2)
解:四边形DMD′N是正方形,理由如下:
∵抛物线y=﹣x2+2x+3与x轴交于A、B两点,
∴令y=0,得﹣x2+2x+3=0,
解得:x1=﹣1,x2=3,
∴A(﹣1,0)、B(3,0),
∴AD= ![]() =2
=2 ![]() ,BD=
,BD= ![]() =2
=2 ![]() ,AB=1+3=4,
,AB=1+3=4,
而AD2+BD2=AB2,
∴△ABD是等腰直角三角形,
∴∠DAB=∠DBA=45°,∠ADB=90°,
由翻折可知:D′M=DM、DN=ND′,
又∵DM=DN,
∴四边形MDND′为菱形,
∵∠MDN=90°,
∴四边形MDND′是正方形;
设DM=DN=t,当点D落在x轴上的点D′处时,
∵四边形MDND′为正方形,
∴∠D′NB=90°,
在Rt△D′NB中,D′N=t,BN=2 ![]() ﹣t,BD′=2,
﹣t,BD′=2,
∴t2+(2 ![]() ﹣t)2=22,
﹣t)2=22,
∴t1=t2= ![]() ,
,
即:经过 ![]() s时,点D恰好落在x轴上的D′处
s时,点D恰好落在x轴上的D′处
(3)
解:存在,
如图,
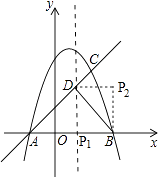
由(2)知△ABD为等腰直角三角形,
∵△PBD与△ABD相似,且不全等,
∴△PBD是以BD为斜边的等腰直角三角形,
∴点P的坐标为(1,0)或(2,3)
【解析】(1)先利用待定系数法求得抛物线和直线的解析式,从而得出对称轴与直线的交点;(2)由抛物线解析式求得点A、B坐标,结合点D坐标可知△ABD为等腰直角三角形,即∠DAB=∠DBA=45°、∠ADB=90°,由翻折性质得D′M=DM、DN=ND′,从而得出四边形MDND′为菱形,根据∠MDN=90°即可得四边形MDND′为正方形;设DM=DN=t,在Rt△D′NB中D′N=t、BN=2 ![]() ﹣t、BD′=2,根据勾股定理即可得出t的值;(3)由△ABD为等腰直角三角形及△PBD与△ABD相似且不全等,知△PBD是以BD为斜边的等腰直角三角形,结合图形即可得答案.
﹣t、BD′=2,根据勾股定理即可得出t的值;(3)由△ABD为等腰直角三角形及△PBD与△ABD相似且不全等,知△PBD是以BD为斜边的等腰直角三角形,结合图形即可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=
 AB中,一定正确的是( )
AB中,一定正确的是( ) 
A.①②③
B.①②④
C.①③④
D.②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景
在数学活动课上,张老师要求同学们拿两张大小不同的矩形纸片进行旋转变换探究活动.如图1,在矩形纸片ABCD和矩形纸片EFGH中,AB=1,AD=2,且EF>AD,FG>AB,点E是AD的中点,矩形纸片EFGH以点E为旋转中心进行逆时针旋转,在旋转过程中会产生怎样的数量关系,提出恰当的数学问题并加以解决.
解决问题
下面是三个学习小组提出的数学问题,请你解决这些问题.
(1)“奋进”小组提出的问题是:如图1,当EF与AB相交于点M,EH与BC相交于点N时,求证:EM=EN.
(2)“雄鹰”小组提出的问题是:在(1)的条件下,当AM=CN时,AM与BM有怎样的数量关系,说明理由.
(3)“创新”小组提出的问题是;若矩形EFGH继续以点E为旋转中心进行逆时针旋转,当∠AEF=60°时,请你在图2中画出旋转后的示意图,并求出此时EF将边BC分成的两条线段的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD,点E是边AB的中点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连接OM、ON、BM、BN.记△MNO、△AOM、△DMN的面积分别为S1、S2、S3 , 则下列结论不一定成立的是( )
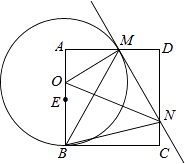
A.S1>S2+S3
B.△AOM∽△DMN
C.∠MBN=45°
D.MN=AM+CN -
科目: 来源: 题型:
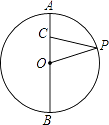
查看答案和解析>>【题目】如图,点C在⊙O的直径AB上,AB=6,AC=1.点P为⊙O上的任意一点,当∠OPC取最大值时,则△OCP的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果10b=n,那么称b为n的劳格数,记为b= d(n).
(1)根据劳格数的定义,可知d(10)=1,d(102)=2,直接写出 d(103)的值.
(2)劳格数有如下运算性质:若m,n为正数,则d(mn)= d(m)+ d(n);d(
 )= d(m)- d(n).
)= d(m)- d(n).根据运算性质,求:
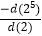 ,若
,若 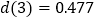 ,直接写出
,直接写出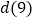 ,
,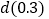 的值.
的值.(3)下表中与数x对应的劳格数
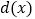 有且只有两个是错误的,请找出错误的劳格数并改正.
有且只有两个是错误的,请找出错误的劳格数并改正. 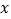
1.5
3
5
6
8
9
12
27
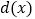
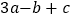
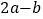
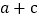

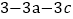
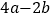
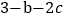
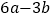
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节,在大明湖举行第七届会民健身运动会龙舟比赛中,甲、乙两队在500米的赛道上,所划行的路程y(m)与时间x(min)之间的函数关系如图所示,下列说法,其中正确的有( )

①乙队比甲队提前0.25min到达终点;
②0.5min后,乙队比甲队每分钟快40m;
③当乙队划行110m时,此时落后甲队15m;
④自1.5min开始,甲队若要与乙队同时到达终点,甲队的速度需要提高到260m/min.
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

