【题目】已知a是最大的负整数,b是-5的相反数,c=![]() ,且a、b、c分别是点A、B、C在数轴上对应的数.若动点P从点A出发沿数轴正方向运动,动点Q同时从点B出发也沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度.
,且a、b、c分别是点A、B、C在数轴上对应的数.若动点P从点A出发沿数轴正方向运动,动点Q同时从点B出发也沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度.
![]()
(1)求a、b、c的值;
(2)P、Q同时出发,求运动几秒后,点P可以追上点Q?
(3)在(2)的条件下,P、Q出发的同时,动点M从点C出发沿数轴正方向运动,速度为每秒6个单位长度,点M追上点Q后立即返回沿数轴负方向运动,追上后点M再运动几秒,M到Q的距离等于M到P距离的两倍?
参考答案:
【答案】(1)a=-1,b=5,c=-3;(2)t=3s;(3)t=![]() 或
或![]() s
s
【解析】
(1)由已知条件即可确定a、b、c的值;
(2)由题意,可知A点表示的数是-1,B点表示的数是5,设运动t秒后,P点对应的数是-1+3t,Q点对应的数是5+t,相遇时两点表示同一个数;
(3),t秒后,M点对应的数是-3+6t,可求M、Q相遇时间,当M向数轴负半轴运动后,M点对应的数是6.6-6(t-1.6)=-6t+16.2,根据题意列出方程7t-11.2=2|9t-17.2|,再结合t的范围求解.
解:(1)∵a是最大的负整数,
∴a=-1,
∵b是-5的相反数,
∴b=5,
∵c=-|-3|,
∴c=-3;
(2)由题意,可知A点表示的数是-1,B点表示的数是5,
设运动t秒后,P点对应的数是-1+3t,Q点对应的数是5+t,
P点追上Q点时,两个点表示的数相同,
∴-1+3t=5+t,
∴t=3,
∴求运动3秒后,点P可以追上点Q;
(3)由(2)知,t秒后,M点对应的数是-3+6t,
当M点追上Q点时,5+t=-3+6t,
∴t=1.6,
此时M点对应的数是6.6,
此后M点向数轴负半轴运动,M点对应的数是6.6-6(t-1.6)=-6t+16.2,
MQ=5+t-(-6t+16.2)=7t-11.2,
MP=|-6t+16.2+1-3t|=|9t-17.2|,
由题意,可得7t-11.2=2|9t-17.2|,
当![]() 时,7t-11.2=18t-34.4,
时,7t-11.2=18t-34.4,
∴t=![]()
当![]() 时,7t-11.2=-18t+34.4,
时,7t-11.2=-18t+34.4,
∴t=![]() ;
;
∴t=![]() 或t=
或t=![]() ,
,
∴![]() ,
,![]() ,
,
∴追上后,再经过![]() s或
s或![]() s,M到Q的距离等于M到P距离的两倍.
s,M到Q的距离等于M到P距离的两倍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”黄金周期间,某风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)(单位:万人),其中9月30日的游客人数为2万:

(1)请问10月2日的游客人数为多少?
(2)请判断7天内游客人数最多的是哪天?最少的是哪天?它们相差多少万人?
(3)求这一次黄金周期间该风景区游客总人数.(假设每天游客都不重复)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣3)+40+(﹣32)+(﹣8)
(2)12﹣(﹣18)+(﹣7)
(3)(+3
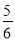 )﹣(﹣5
)﹣(﹣5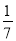 )+(﹣2
)+(﹣2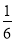 )﹣(﹣32
)﹣(﹣32 )
)(4)81.26﹣293.8+8.74+111
-
科目: 来源: 题型:
查看答案和解析>>【题目】请根据图示的对话解答下列问题.

求:(1)a,b的值;
(2)8﹣a+b﹣c的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,3),点B的坐标为(n,1).
的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,3),点B的坐标为(n,1).(1)求n的值,并结合图象,直接写出不等式
 <kx+b的解集;
<kx+b的解集;(2)点E为x轴上一个动点,若S△AEB=6,求点E的坐标.

相关试题

