【题目】如图,反比例函数y=![]() 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,3),点B的坐标为(n,1).
的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,3),点B的坐标为(n,1).
(1)求n的值,并结合图象,直接写出不等式![]() <kx+b的解集;
<kx+b的解集;
(2)点E为x轴上一个动点,若S△AEB=6,求点E的坐标.

参考答案:
【答案】(1)n=6,x<0或2<x<6;(2)E点坐标为(8,0)或(﹣4,0).
【解析】
(1)先把A点坐标代入y=![]() 求出m得到反比例函数解析式为y=
求出m得到反比例函数解析式为y=![]() ,再把B(n,1)代入y=
,再把B(n,1)代入y=![]() 可求出n,然后利用函数图象写出一次函数图象在反比例函数图象上方所对应的自变量的范围即可;
可求出n,然后利用函数图象写出一次函数图象在反比例函数图象上方所对应的自变量的范围即可;
(2)易得直线AB的解析式为y=﹣![]() x+4,再求出直线AB与x轴的交点坐标为(2,0),设E(x,0),利用三角形面积公式得到
x+4,再求出直线AB与x轴的交点坐标为(2,0),设E(x,0),利用三角形面积公式得到![]() ×|x﹣2|×(3﹣1)=6,然后解方程求出x即可得到E点坐标.
×|x﹣2|×(3﹣1)=6,然后解方程求出x即可得到E点坐标.
(1)把A(2,3)代入y=![]() 得m=2×3=6,
得m=2×3=6,
∴反比例函数解析式为y=![]() ,
,
把B(n,1)代入y=![]() 得n=6,
得n=6,
当2<x<6或x<0时,![]() <kx+b,
<kx+b,
即不等式![]() <kx+b的解集为x<0或2<x<6;
<kx+b的解集为x<0或2<x<6;
(2)易得直线AB的解析式为y=﹣![]() x+4,
x+4,
当x=0时,﹣![]() x+4=0,解得x=8,则直线AB与x轴的交点坐标为(8,0)
x+4=0,解得x=8,则直线AB与x轴的交点坐标为(8,0)
设E(x,0),
∴![]() ×|x﹣8|×(3﹣1)=6,解得x=14或x=2
×|x﹣8|×(3﹣1)=6,解得x=14或x=2
∴E点坐标为(14,0)或(2,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是最大的负整数,b是-5的相反数,c=
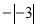 ,且a、b、c分别是点A、B、C在数轴上对应的数.若动点P从点A出发沿数轴正方向运动,动点Q同时从点B出发也沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度.
,且a、b、c分别是点A、B、C在数轴上对应的数.若动点P从点A出发沿数轴正方向运动,动点Q同时从点B出发也沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度.
(1)求a、b、c的值;
(2)P、Q同时出发,求运动几秒后,点P可以追上点Q?
(3)在(2)的条件下,P、Q出发的同时,动点M从点C出发沿数轴正方向运动,速度为每秒6个单位长度,点M追上点Q后立即返回沿数轴负方向运动,追上后点M再运动几秒,M到Q的距离等于M到P距离的两倍?
-
科目: 来源: 题型:
查看答案和解析>>【题目】请根据图示的对话解答下列问题.

求:(1)a,b的值;
(2)8﹣a+b﹣c的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.

(1)过点C画线段AB的平行线CD;
(2)过点A画线段BC的垂线,垂足为E;
(3)线段AE的长度是点 到直线 的距离;
(4)比较线段AE、AB、BC的大小关系(用“<”连接).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
数轴上线段的长度可以用线段端点表示的数进行减法运算得到,例如图,线段AB=1=0﹣(﹣1);线段 BC=2=2﹣0;线段 AC=3=2﹣(﹣1)问题
①数轴上点M、N代表的数分别为﹣9和1,则线段MN= ;
②数轴上点E、F代表的数分别为﹣6和﹣3,则线段EF= ;
③数轴上的两个点之间的距离为5,其中一个点表示的数为2,则另一个点表示的数为m,求m.
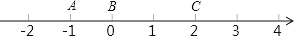
-
科目: 来源: 题型:
查看答案和解析>>【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

相关试题

