【题目】在□ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
参考答案:
【答案】(1)见解析(2)见解析
【解析】
试题(1)根据平行四边形的性质,可得AB与CD的关系,根据平行四边形的判定,可得BFDE是平行四边形,再根据矩形的判定,可得答案;
(2)根据平行线的性质,可得∠DFA=∠FAB,根据等腰三角形的判定与性质,可得∠DAF=∠DFA,根据角平分线的判定,可得答案.
试题(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DFA=∠FAB.
在Rt△BCF中,由勾股定理,得
BC=![]() =
=![]() =5,
=5,
∴AD=BC=DF=5,
∴∠DAF=∠DFA,
∴∠DAF=∠FAB,
即AF平分∠DAB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,AC,BD是对角线。将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG。则下列结论:①四边形AEGF是菱形;②△AED≌△GED;③∠DFG=112.5°;④BC+FG=1.5.其中正确的结论是( )
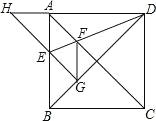
A. ①②③④ B. ①②③ C. ①② D. ②
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知AB=10,点C、D在线段AB上且AC=DB=2; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连结EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是________.
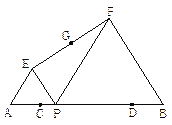
-
科目: 来源: 题型:
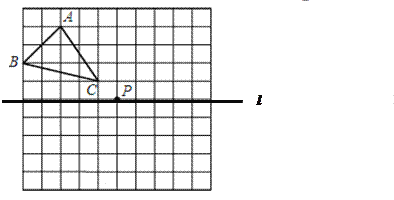
查看答案和解析>>【题目】如图,一个10×10网格,每个小正方形的边长均为1,每个小正方形的顶点叫格点,△ABC的顶点均在格点上.
(1)画出△ABC关于直线l的对称的△A1B1C1.
(2)画出△ABC关于点P的中心对称图形△A2B2C2.
(3)△A1B1C1与△A2B2C2组成的图形_______________(是或否)轴对称图形,如果是轴对称图形,请画出对称轴.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:

(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,△ABC是等边三角形,点D是边BC上任意一点(不与B、C重合),点E在边AC上,∠ADE=60°,∠BAD与∠CDE有怎样的数量关系,并给予证明.
(2)如图②,在△ABC中,AB=AC,点D是边BC上一点(不与B、C重合), ∠ADE=∠B,点E在边AC上.若CE=BD=3,BC=8,求AB的长度.

相关试题

