【题目】抛物线![]() (
(![]() )的部分图象如图所示,与
)的部分图象如图所示,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() ,下列结论是:①
,下列结论是:①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;④
有两个不相等的实数根;④![]() ;⑤若点
;⑤若点![]() 在该抛物线上,则
在该抛物线上,则![]() ,其中正确的个数有( )
,其中正确的个数有( )
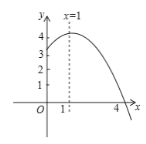
A.1个B.2个C.3个D.4个
参考答案:
【答案】D
【解析】
根据二次函数的对称性补全图像,再根据二次函数的性质即可求解.
如图,∵与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() ,
,
实验求出二次函数与x轴的另一个交点为(-2,0)
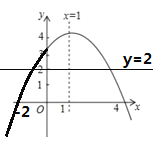
故可补全图像如下,
由图可知a<0,c>0,对称轴x=1,故b>0,
∴![]() ,①错误,
,①错误,
②对称轴x=1,故x=-![]() ,∴
,∴![]() ,正确;
,正确;
③如图,作y=2图像,与函数有两个交点,∴方程![]() 有两个不相等的实数根,正确;④∵x=-2时,y=0,即
有两个不相等的实数根,正确;④∵x=-2时,y=0,即![]() ,正确;⑤∵抛物线的对称轴为x=1,故点
,正确;⑤∵抛物线的对称轴为x=1,故点![]() 在该抛物线上,则
在该抛物线上,则![]() ,正确;
,正确;
故选D
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是昌平区2019年1月份每天的最低和最高气温,观察此图,下列说法正确的是( )

A.在1月份中,最高气温为10℃,最低气温为-2℃
B.在10号至16号的气温中,每天温差最小为7℃
C.每天的最高气温均高于0℃,最低气温均低于0℃
D.每天的最高气温与最低气温都是具有相反意义的量
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由一个角为60°且边长为1的菱形组成的网格,每个菱形的顶点称为格点,点A,B,C都在格点上,则tan∠BAC=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD内找一点O,使它到四边形四个顶点的距离之和OA+OB+OC+OD最小,正确的作法是连接AC、BD交于点O,则点O就是要找的点,请你用所学过的数学知识解释这一道理__________________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为灾区开展了“献出我们的爱”赈灾捐款活动,九年级(1)班50名同学积极参加了这次赈灾捐款活动,因不慎,表中数据有一处被墨水污染,已无法看清,但已知全班平均每人捐款38元.
捐款(元)
10
15
30
50
60
人数
3
6
11
11
13
6
(1)根据以上信息可知,被污染处的数据为 .
(2)该班捐款金额的众数为 ,中位数为 .
(3)如果用九年级(1)班捐款情况作为一个样本,请估计全校2000人中捐款在40元以上(包括40元)的人数是多少?
-
科目: 来源: 题型:
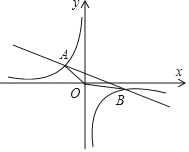
查看答案和解析>>【题目】如图,反比例函数y=
 (k≠0)的图象与一次函数y=﹣
(k≠0)的图象与一次函数y=﹣ x+1的图象交于A(﹣2,m),B(n,﹣1)两点.
x+1的图象交于A(﹣2,m),B(n,﹣1)两点.(1)求反比例函数的解析式;
(2)连接OA,OB,求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们可用
 表示以
表示以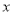 为自变量的函数,如一次函数
为自变量的函数,如一次函数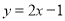 ,可表示为
,可表示为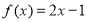 ,且
,且 ,
,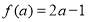 ,定义:若存在实数
,定义:若存在实数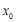 ,使
,使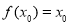 成立,则称
成立,则称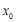 为
为 的不动点,例如:
的不动点,例如: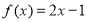 ,令
,令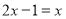 ,得
,得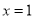 ,那么
,那么 的不动点是1.
的不动点是1.(1)已知函数
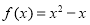 ,求
,求 的不动点.
的不动点.(2)函数
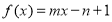 (
(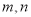 是常数)的图象上存在不动点吗?若存在,请求出不动点;若不存在,请说明理由;
是常数)的图象上存在不动点吗?若存在,请求出不动点;若不存在,请说明理由;(3)已知函数
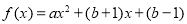 (
(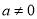 ),当
),当 时,若一次函数
时,若一次函数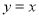 与二次函数
与二次函数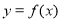 的交点为
的交点为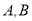 ,即
,即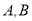 两点的横坐标是函数
两点的横坐标是函数 的不动点,且
的不动点,且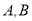 两点关于直线
两点关于直线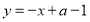 对称,求
对称,求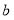 的取值范围.
的取值范围.
相关试题

