搜索
【题目】如图，在四边形ABCD内找一点O，使它到四边形四个顶点的距离之和OA+OB+OC+OD最小，正确的作法是连接AC、BD交于点O，则点O就是要找的点，请你用所学过的数学知识解释这一道理__________________________.
参考答案：
【答案】两点之间线段最短.
【解析】
已知OA+OB+OC+OD＝(OA+OC)+(OB+OD),由图形可知，当(OA+OC)最短时即点O在线段AC上，同理要使(OB+OD)最短，则O在线段BD上，使四条线段和最短即为AC、BD交点，利用的是两点之间线段最短.
解：由题意可知，因为两点之间线段最短，所以当点O在线段AC上时(OA+OC)最短，同理可得O在线段BD上时，(OB+OD)最短，可得点O就是要找的点，依据就是两点之间线段最短；
故答案为：两点之间线段最短.
-
科目： 来源： 题型：
查看答案和解析>>【题目】勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理，但远在毕达哥拉斯出生之前，这一定理早已被人们所利用，世界上各个文明古国都对勾股定理的发现和研究作出过贡献（希腊、中国、埃及、巴比伦、印度等），特别是定理的证明，据说有400余种方法．其中在《几何原本》中有一种证明勾股定理的方法：如图所示，作CG⊥FH，垂足为G，交AB于点P，延长FA交DE于点S，然后将正方形ACED、正方形BCNM作等面积变形，得S正方形ACED=SACQS，S正方形BCNM=SBCQT，这样就可以完成勾股定理的证明．对于该证明过程，下列结论错误的是（ ）
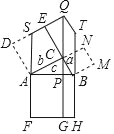
A. △ADS≌△ACB B. SACQS=S矩形APGF
C. SCBTQ=S矩形PBHG D. SE=BC
-
科目： 来源： 题型：
查看答案和解析>>【题目】下图是昌平区2019年1月份每天的最低和最高气温，观察此图，下列说法正确的是（ ）
A.在1月份中，最高气温为10℃，最低气温为－2℃
B.在10号至16号的气温中，每天温差最小为7℃
C.每天的最高气温均高于0℃，最低气温均低于0℃
D.每天的最高气温与最低气温都是具有相反意义的量
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是由一个角为60°且边长为1的菱形组成的网格，每个菱形的顶点称为格点，点A，B，C都在格点上，则tan∠BAC=_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线
（
）的部分图象如图所示，与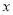
轴的一个交点坐标为
，抛物线的对称轴是
，下列结论是：①
；②
；③方程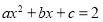
有两个不相等的实数根；④
；⑤若点
在该抛物线上，则
，其中正确的个数有（ ）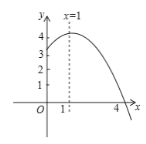
A.1个B.2个C.3个D.4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校为灾区开展了“献出我们的爱”赈灾捐款活动，九年级（1）班50名同学积极参加了这次赈灾捐款活动，因不慎，表中数据有一处被墨水污染，已无法看清，但已知全班平均每人捐款38元.
捐款（元）
10
15
30
50
60
人数
3
6
11
11
13
6
（1）根据以上信息可知，被污染处的数据为 .
（2）该班捐款金额的众数为 ，中位数为 .
（3）如果用九年级（1）班捐款情况作为一个样本，请估计全校2000人中捐款在40元以上（包括40元）的人数是多少？
-
科目： 来源： 题型：
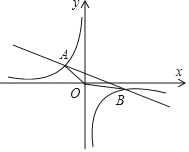
查看答案和解析>>【题目】如图，反比例函数y=
（k≠0）的图象与一次函数y=﹣
x+1的图象交于A（﹣2，m），B（n，﹣1）两点．（1）求反比例函数的解析式；
（2）连接OA，OB，求△AOB的面积．
相关试题
