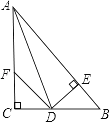
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
求证:(1)CF=EB.
(2)AB=AF+2EB.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)利用HL证明RT△CDF≌RT△EDB即可得出CF=EB;
(2)利用HL证明RT△ADE≌RT△ADC即可得出AC=AE,再由AB=AE+EB=AF+CF+EB进行等量代换即可.
(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴DE=DC,
在Rt△CDF和Rt△EDB中,
![]() ,
,
∴Rt△CDF≌Rt△EDB(HL)
∴CF=EB
(2)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴CD=DE.
在△ADC与△ADE中,![]() ,
,
∴△ADC≌△ADE(HL),
∴AC=AE,∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,线段AD=10cm,点B,C都是线段AD上的点,且AC=7cm,BD=4cm,若E,F分别是线段AB,CD的中点,求BC与EF的长度.

-
科目: 来源: 题型:
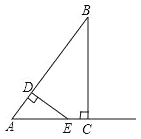
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点D从点A出发以每秒3个单位的速度运动至点B,过点D作DE⊥AB交射线AC于点E.设点D的运动时间为t秒(t>0).
(1)线段AE的长为 .(用含t的代数式表示)
(2)若△ADE与△ACB的面积比为1:4时,求t的值.
(3)设△ADE与△ACB重叠部分图形的周长为L,求L与t之间的函数关系式.
(4)当直线DE把△ACB分成的两部分图形中有一个是轴对称图形时,直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的大小;
(2)若CD=3,求DF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1. 其余每个数均为其上方左右两数之和,它给出了(a+b) n (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律. 例如. 在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数 1,3,3,1,恰好对应着(a+b) 3= a3+3a2b+3ab2+b3展开式中的系数等等.

(1)根据上面的规律,写出第五行的五个数
(2)根据上面的规律,写出(a+b) 5的展开式.
(3)利用上面的规律计算:35-5×34+10×33-10×32+5×3-1 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】公园的门票价格规定如下表:
购票张数
1 到 50 张
51 到 100 张
101 到 150张
150 张以上
每张票的价格
12 元
10 元
8 元
超过 150 张的部分 7 元
某校七年级(1)(2)两个班共 104 人,其中(1)班 40 多人,不足 50 人,经估算,如果两个班都以班为单位购票,则一共应付 1136 元,问:
(1)若两班联合起来作为一个团体购票,可省多少钱?
(2)两班学生各有多少人?
(3)若七年级(3)班有 n 人(46<n<55)与(1),(2)班一起去游园,某商家赞助,支付三个班的所有门票费,则该商家最少花费 元(用含 n 的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形
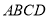 ,长
,长 ,宽
,宽 ,
, 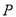 、
、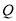 分别是
分别是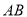 、
、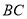 上运动的两点。若
上运动的两点。若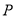 自点
自点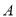 出发,以
出发,以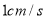 的速度沿
的速度沿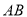 方向运动,同时,
方向运动,同时, 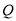 自点
自点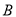 出发以
出发以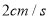 的速度沿
的速度沿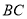 方向运动,则经过____________秒,以
方向运动,则经过____________秒,以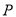 、
、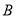 、
、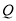 为顶点的三角形与
为顶点的三角形与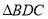 相似。
相似。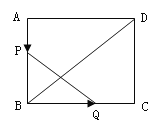
相关试题

