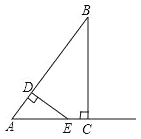
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点D从点A出发以每秒3个单位的速度运动至点B,过点D作DE⊥AB交射线AC于点E.设点D的运动时间为t秒(t>0).
(1)线段AE的长为 .(用含t的代数式表示)
(2)若△ADE与△ACB的面积比为1:4时,求t的值.
(3)设△ADE与△ACB重叠部分图形的周长为L,求L与t之间的函数关系式.
(4)当直线DE把△ACB分成的两部分图形中有一个是轴对称图形时,直接写出t的值.
参考答案:
【答案】(1)5t;(2)![]() ;(3)当
;(3)当![]() 时,L=12t,当
时,L=12t,当![]() 时,
时, ![]() ;(4)
;(4)![]() 或1.
或1.
【解析】【试题分析】(1)利用三角函数求解;(2)根据△ADE与△ACB的面积比为1:4列出方程求解;(3)按照![]() 和
和![]() 两种情况讨论; (4)当DE=CE时,四边形BCED是轴对称图形,和当DE和BC相交于F,AD=AC时,四边形ACFE是轴对称图形两种情形讨论.
两种情况讨论; (4)当DE=CE时,四边形BCED是轴对称图形,和当DE和BC相交于F,AD=AC时,四边形ACFE是轴对称图形两种情形讨论.
【试题解析】
(1)在Rt△ABC中,tanA=![]() =
=![]()
由题意得,AD=3t,
在Rt△ADE中,tanA=![]() =
=![]() =
=![]() ,
,
根据勾股定理得,AE=5t.
故答案为5t;
(2)方法一:∵ED⊥AB,
∴∠ADE=90°.∵∠ACB=90°,
∴∠ACB=∠ADE.∠A=∠A,
∴△ABC∽△AED,
∴![]() .
.
∵AD=3t,AC=3,BC=4,
∴DE=4t.
∴![]() .
.
∵![]() ,
,
∵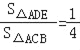 ,
,
∴![]() .
.
∴![]() (舍)
(舍)
∴t的值为![]() .
.
方法二:∵ED⊥AB,
∴∠ADE=90°.
∵∠ACB=90°,
∴∠ACB=∠ADE.
∵∠A=∠A,
∴△ABC∽△AED,
∵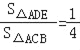 ,
,
∴![]() .
.
∵AC=3,AD=3t,
∴2×3t=3,t=![]() .
.
(3)由(2)得:△ABC∽△AED,
∴![]() .
.
∵AD=3t,
∴DE=4t,AE=5t.BD=5﹣3t,
∴当![]() 时,L=3t+4t+5t=12t.
时,L=3t+4t+5t=12t.
∴L=12t.
当![]() 时,如图,
时,如图,
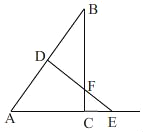
∵∠B=∠B,∠BDF=∠BCA,
∴△ABC∽△FBD,
∴![]() .
.
∵BD=5﹣3t,
∴![]() .
.
∵∠BFD=∠EFC,∠BDF=∠ECF,
∴∠B=∠E,
∵∠FCE=∠BCA
∴△BCA∽△ECF,
∴![]() .
.
∵CE=5t﹣3,
∴![]() .
.
![]() .
.
∴![]() .
.
(4)由(1)知,AE=5t,DE=4t,
∴CE=3﹣5t,
当DE=CE时,四边形BCED是轴对称图形,
∴4t=3﹣5t,
∴t=![]() ,
,
当DE和BC相交于F,AD=AC时,四边形ACFE是轴对称图形,
∵AD=3t,AC=3,
∴3t=3,
∴t=1.
即:满足条件的时间t为![]() 或1.
或1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90° 时,可知△ABP∽△PCD.(不要求证明)
(1)探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.
(2)拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上若∠B=∠C=∠DPE=45°,BC=8
 ,CE=6,则DE的长为 .
,CE=6,则DE的长为 .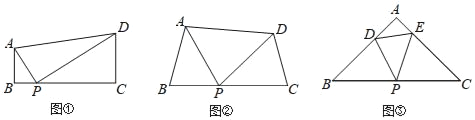
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.
(1)如图1,△ABC是等腰锐角三角形,AB=AC(
 ),若∠ABC的角平分线BD交AC于点D,且BD是△ABC的一条特异线,则∠BDC=______度;
),若∠ABC的角平分线BD交AC于点D,且BD是△ABC的一条特异线,则∠BDC=______度;(2)如图2,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.求证:AE是△ABC的一条特异线;
(3)如图3,已知△ABC是特异三角形,且∠A=30°,∠B为钝角,求出所有可能的∠B的度数(如有需要,可在答题卡相应位置另外画图).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,线段AD=10cm,点B,C都是线段AD上的点,且AC=7cm,BD=4cm,若E,F分别是线段AB,CD的中点,求BC与EF的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的大小;
(2)若CD=3,求DF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
求证:(1)CF=EB.
(2)AB=AF+2EB.
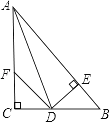
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1. 其余每个数均为其上方左右两数之和,它给出了(a+b) n (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律. 例如. 在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数 1,3,3,1,恰好对应着(a+b) 3= a3+3a2b+3ab2+b3展开式中的系数等等.

(1)根据上面的规律,写出第五行的五个数
(2)根据上面的规律,写出(a+b) 5的展开式.
(3)利用上面的规律计算:35-5×34+10×33-10×32+5×3-1 .
相关试题

