【题目】公园的门票价格规定如下表:
购票张数 | 1 到 50 张 | 51 到 100 张 | 101 到 150张 | 150 张以上 |
每张票的价格 | 12 元 | 10 元 | 8 元 | 超过 150 张的部分 7 元 |
某校七年级(1)(2)两个班共 104 人,其中(1)班 40 多人,不足 50 人,经估算,如果两个班都以班为单位购票,则一共应付 1136 元,问:
(1)若两班联合起来作为一个团体购票,可省多少钱?
(2)两班学生各有多少人?
(3)若七年级(3)班有 n 人(46<n<55)与(1),(2)班一起去游园,某商家赞助,支付三个班的所有门票费,则该商家最少花费 元(用含 n 的式子表示)
参考答案:
【答案】(1)304元;(2)七年级(1)班有48人,七年级(2)班有56人;(3)(7n+1178).
【解析】
(1)先求出购团体票的费用,再用1136元-团体票的费用就是节约的钱;
(2)设七年级(1)班有x人,则七年级(2)班有(104-x)人,根据两个班共付费1136元建立方程求出其解就可以;
(3)表示出总人数,判断范围,分段列式计算即可.
(1)由题意,得
1136104×8=304元.
答:两班联合起来,作为一个团体购票,可省304元;
(2)设七年级(1)班有x人,则七年级(2)班有(104x)人,由题意,得
12x+10(104x)=1136,
解得:x=48,
∴七年级(2)班有学生:10448=56人.
答:七年级(1)班有48人,则七年级(2)班有56人;
(3)由题知,三个班总人数为(104+n)人,
∵46<n<55,
∴104+n>150,
∴费用为:![]()
![]() 元
元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的大小;
(2)若CD=3,求DF的长.

-
科目: 来源: 题型:
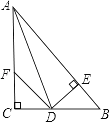
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
求证:(1)CF=EB.
(2)AB=AF+2EB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1. 其余每个数均为其上方左右两数之和,它给出了(a+b) n (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律. 例如. 在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数 1,3,3,1,恰好对应着(a+b) 3= a3+3a2b+3ab2+b3展开式中的系数等等.

(1)根据上面的规律,写出第五行的五个数
(2)根据上面的规律,写出(a+b) 5的展开式.
(3)利用上面的规律计算:35-5×34+10×33-10×32+5×3-1 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形
 ,长
,长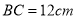 ,宽
,宽 ,
, 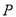 、
、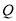 分别是
分别是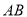 、
、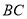 上运动的两点。若
上运动的两点。若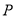 自点
自点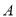 出发,以
出发,以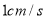 的速度沿
的速度沿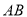 方向运动,同时,
方向运动,同时, 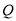 自点
自点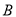 出发以
出发以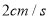 的速度沿
的速度沿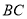 方向运动,则经过____________秒,以
方向运动,则经过____________秒,以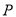 、
、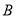 、
、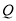 为顶点的三角形与
为顶点的三角形与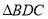 相似。
相似。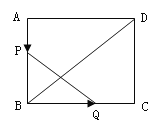
-
科目: 来源: 题型:
查看答案和解析>>【题目】供电局的电力维修工要到30千米远的郊区进行电力抢修.技术工人骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果他们同时到达.已知抢修车的速度是摩托车的1.5倍,求这两种车的速度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①,图②都是4×6的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,且点A,B均在格点上.

(1)在图①中以AB为对角线画出一个矩形,使矩形的另外两个顶点也在格点上,且所画的矩形不是正方形;
(2)在图②中以AB为对角线画出一个菱形,使菱形的另外两个顶点也在格点上,且所画的菱形不是正方形;
(3)图①中所画的矩形的面积为 ;图②中所画的菱形的周长为 .
相关试题

