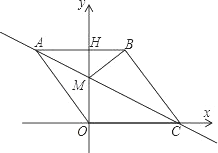
【题目】如图,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(-3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
(1)求直线AC的解析式;
(2)动点P从点A出发,沿折线ABC的方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围);
(3)动点P从点A出发,沿线段AB方向以2个单位/秒的速度向终点B匀速运动,当∠MPB与∠BCO互为余角时,试确定t的值.
参考答案:
【答案】(1)直线AC的解析式为y=-![]() x+
x+![]() .(2)S=-
.(2)S=-![]() t+
t+![]() (0≤t<
(0≤t<![]() ).S=
).S=![]() t-
t-![]() (
(![]() <t≤5);(3)t=
<t≤5);(3)t=![]() .
.
【解析】
试题分析:(1)过点A作AE⊥x轴,垂足为E,根据勾股定理求出OA的长,根据菱形的性质可得出C点坐标,再利用待定系数法求出直线AC的解析式即可;
(2)先求出OM的长,再分点P在AB边上运动与点P在BC边上运动两种情况进行分类讨论;
(3)先根据菱形的性质及三角形内角和定理得出∠MPB=∠ABM,再根据等腰三角形的性质即可得出结论.
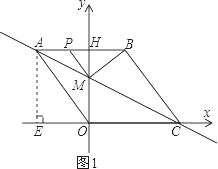
试题解析:(1)如图1,过点A作AE⊥x轴,垂足为E.

∵A(-3,4),
∴AE=4,OE=3,
∴OA=![]() =5.
=5.
∵四边形ABCO是菱形,
∴OC=CB=BA=OA=5,
∴C(5,0).设直线AC的解析式为y=kx+b,将A(-3,4),C(5,0)代入得:![]() ,
,
解得 ,
,
∴直线AC的解析式为y=-![]() x+
x+![]() .
.
(2)由(1)得点M的坐标为(0,![]() ),
),
∴OM=![]() .
.
如图1,当点P在AB边上运动时.
由题意得OH=4,
∴HM=![]() .
.
∴S=![]() BP
BP![]() MH=
MH=![]() (5-2t)×
(5-2t)×![]()
∴S=-![]() t+
t+![]() (0≤t<
(0≤t<![]() ).
).
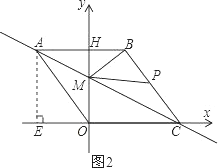
如图2,当点P在BC边上运动时.
∵∠OCM=∠BCM,OC=BC,MC=MC.
∴△MOC≌△MBC.
∴BM=OM=![]() ,∠MBC=∠MOC=90°.
,∠MBC=∠MOC=90°.
∴S=![]() BP
BP![]() BM=
BM=![]() (2t-5)×
(2t-5)×![]()
∴S=![]() t-
t-![]() (
(![]() <t≤5);
<t≤5);
(3)∵∠AOC=∠ABC,∠MOC=∠MBC,
∴∠AOM=∠ABM.
∵∠MPB+∠BCO=90°,∠BAO=∠BCO,∠BAO+∠AOM=90°.
∴∠MPB=∠AOM,
∴∠MPB=∠ABM.
如图3,当点P在AB边上运动时.
∵∠MPB=∠ABM,
∴PM=BM.
∵MH⊥PB,
∴PH=HB=5-3=2,
∴PA=3-2=1.
∴t=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2+bx+c与y轴交于点C,与x轴交于点A、B,且AB=2,抛物线的对称轴为直线x=2;
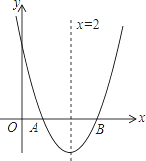
(1)求抛物线的函数表达式;
(2)如果抛物线的对称轴上存在一点P,使得△APC周长的值最小,求此时P点坐标及△APC周长;
(3)设D为抛物线上一点,E为对称轴上一点,若以点A、B、D、E为顶点的四边形是平行四边形,求点D的坐标.(直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,延长BO交⊙O于点A,点D为⊙O上一点,过点A作直线BD的垂线,垂足为C,AD平分∠BAC.
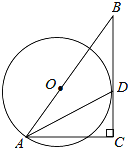
(1)求证:BC是⊙O的切线;
(2)求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( )

A.130° B.150° C.160° D.170°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=
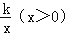 经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=9,则S△OBD的值为 .
经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=9,则S△OBD的值为 .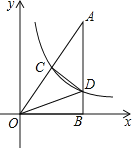
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人沿同一路线登山,图中线段OC、折线OAB分别是甲、乙两人登山的路程y(米)与登山时间x(分)之间的函数图象.请根据图象所提供的信息,解答如下问题:
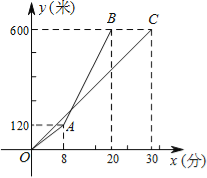
(1)求甲登山的路程与登山时间之间的函数关系式,并写出自变量x的取值范围;
(2)求乙出发后多长时间追上甲?此时乙所走的路程是多少米?
相关试题

