Question

【题目】如图，在Rt△ABC中，∠ACB＝90°，BC＝30cm，AC＝40cm，点D在线段AB上，从点B出发，以2cm/s的速度向终点A运动，设点D的运动时间为t秒。

（1）点D在运动t秒后，BD＝ cm（用含有t的式子表示）

（2）AB＝cm，AB边上的高为cm；

（3）点D在运动过程中，当△BCD为等腰三角形时，求t的值．

Answer 1

【答案】（1）；（2）50；24；（3）t的值为15s或18s或12.5s.

【解析】

（1）根据点D以2cm/s的速度向终点A运动，设点D的运动时间为t秒，即可表示出；

（2）利用勾股定理求出AB的长，再利用三角形面积公式即可求得AB边上的高；

（3）分三种情况：①当BD=BC=30cm时得到2t=30，即可得到结果；

②当CD=CB=30cm时，作CE⊥AB于E，则，由（1）得CE=24，由勾股定理求出BE，即可得出结果；

③当DB=DC时，∠BCD=∠B，证明DA=DC，得出AD=DB=AB，即可得出结果.

（1） ∵点D以2cm/s的速度向终点A运动，设点D的运动时间为t秒

∴

故答案为：

（2）由勾股定理得，

设AB边上的高为h，

∴，

解得：

故答案为：50；24.

（3） 分三种情况：

①当BD=BC=30cm时，2t=30

∴t=15（s）

②当CD=CB=30cm时，作CE⊥AB于E，如图所示：

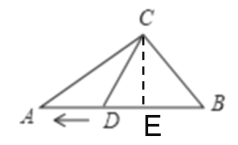
则

由（2）得，AB边上的高CE=24，

在中，由勾股定理得：

∴

③当DB=DC时，∠BCD=∠B

∵∠A=90°﹣∠B，∠ACD=90°﹣∠BCD，

∴∠ACD=∠A

∴DA=DC

∴AD=DB=AB=25（cm）

∴

综上所述，t的值为15s或18s或12.5s.