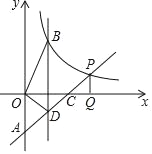
【题目】直线y=x﹣2与两坐标轴分别交于点A,C,交y=![]() (x>0)于点P,PQ⊥x轴于点Q,CQ=1.
(x>0)于点P,PQ⊥x轴于点Q,CQ=1.
(1)求反比例函数解析式;
(2)平行于y轴的直线x=m分别交y=x﹣2,y=![]() (x>0)于点D,B(B在线段AP上方),若S△BOD=2,求m值.
(x>0)于点D,B(B在线段AP上方),若S△BOD=2,求m值.
参考答案:
【答案】(1)反比例函数解析式为y=![]() ;(2)m=1.
;(2)m=1.
【解析】
(1)由题意,可以求出C点的坐标,再根据CQ=1,可以求出Q点的坐标,又PQ⊥x轴于点Q,P在直线上,可求出P点的坐标,故k值易求.
(2)题意可设点B坐标为(m,![]() ),点D坐标为(m,m﹣2),用含m的代数可以表示BD和S△BOD,再依据S△BOD=2,得到一个关于m的方程,即可求出m的值.
),点D坐标为(m,m﹣2),用含m的代数可以表示BD和S△BOD,再依据S△BOD=2,得到一个关于m的方程,即可求出m的值.
(1)在y=x﹣2中,当y=0时,x=2,
∴C(2,0),
而CQ=1,
∴Q(3,0),
当x=3时,y=3﹣2=1,则P(3,1),
把P(3,1)代入y=![]() 得k=3×1=3,
得k=3×1=3,
∴反比例函数解析式为y=![]() ;
;
(2)由题意可得点B坐标为(m,![]() ),点D坐标为(m,m﹣2),
),点D坐标为(m,m﹣2),
∴BD=![]() ﹣m+2,
﹣m+2,
∵S△BOD=2,
∴![]() (
(![]() ﹣m+2)m=2.
﹣m+2)m=2.
解得m=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列从左边到右边的变形,是因式分解的是( )
A.y
 ﹣5y﹣6=(y﹣6)(y+1)B.a
﹣5y﹣6=(y﹣6)(y+1)B.a +4a﹣3=a(a+4)﹣3
+4a﹣3=a(a+4)﹣3C.x(x﹣1)=x
 ﹣xD.m
﹣xD.m +n
+n =(m+n)(m﹣n)
=(m+n)(m﹣n) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,面积为4的正方形OABC的顶点O与坐标原点重合,边OA、OC分别在x轴、y轴的正半轴上,点B、P都在函数y=
 (x>0)的图象上,过动点P分别作轴x、y轴的平行线,交y轴、x轴于点D、E.设矩形PDOE与正方形OABC重叠部分图形的面积为S,点P的横坐标为m.
(x>0)的图象上,过动点P分别作轴x、y轴的平行线,交y轴、x轴于点D、E.设矩形PDOE与正方形OABC重叠部分图形的面积为S,点P的横坐标为m.(1)求k的值;
(2)用含m的代数式表示CD的长;
(3)求S与m之间的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+2与x轴,y轴分别交于点A(﹣1,0)和点B,与反比例函数y=
 的图象在第一象限内交于点C(1,n).
的图象在第一象限内交于点C(1,n).(1)求一次函数y=kx+2与反比例函数y=
 的表达式;
的表达式;(2)过x轴上的点D(a,0)作平行于y轴的直线l(a>1),分别与直线y=kx+2和双曲线y=
 交于P、Q两点,且PQ=2QD,求点D的坐标.
交于P、Q两点,且PQ=2QD,求点D的坐标.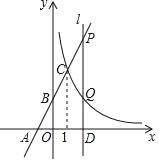
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填写下表,观察被开方数
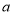 的小数点与算术平方根
的小数点与算术平方根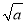 的小数点的移动规律:
的小数点的移动规律: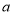
0.0016
0.16
16
1600
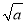
0.04
0.4
(2)根据你发现的规律填空:
①已知
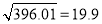 ,则
,则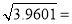 .
.②已知
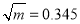 ,
,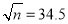 ,则
,则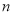 是
是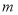 的 倍.
的 倍. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“奇巧数”,如
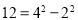 ,
, ,
,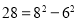 ,,因此
,,因此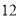 ,
,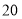 ,
,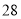 都是奇巧数.
都是奇巧数.(1)
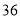 ,
,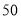 是奇巧数吗?为什么?
是奇巧数吗?为什么?(2)设两个连续偶数为
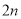 ,
,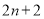 (其中
(其中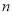 为正整数),由这两个连续偶数构造的奇巧数是4的倍数吗?为什么?
为正整数),由这两个连续偶数构造的奇巧数是4的倍数吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】材料:一般地,若
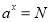 (
(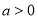 且
且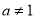 ),那么
),那么 叫做以
叫做以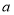 为底
为底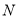 的对数,记作
的对数,记作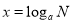 ,比如指数式
,比如指数式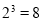 可以转化为对数式
可以转化为对数式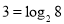 ,对数式
,对数式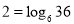 可以转化为指数式
可以转化为指数式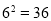 .
.根据以上材料,解决下列问题:
(1)计算:
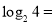 ,
,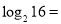 ,
,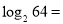 ;
;(2)观察(1)中的三个数,猜测:
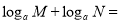 (
(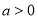 且
且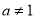 ,
,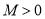 ,
, ),并加以证明这个结论;
),并加以证明这个结论;(3)已知:
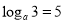 ,求
,求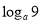 和
和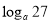 的值(
的值(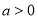 且
且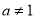 ).
).
相关试题

