【题目】材料:一般地,若![]() (
(![]() 且
且![]() ),那么
),那么![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记作
的对数,记作![]() ,比如指数式
,比如指数式![]() 可以转化为对数式
可以转化为对数式![]() ,对数式
,对数式![]() 可以转化为指数式
可以转化为指数式![]() .
.
根据以上材料,解决下列问题:
(1)计算:![]() ,
,![]() ,
,![]() ;
;
(2)观察(1)中的三个数,猜测:![]() (
(![]() 且
且![]() ,
,![]() ,
,![]() ),并加以证明这个结论;
),并加以证明这个结论;
(3)已知:![]() ,求
,求![]() 和
和![]() 的值(
的值(![]() 且
且![]() ).
).
参考答案:
【答案】(1)2,4,6;(2)![]() ,证明见解析;(3)10,15.
,证明见解析;(3)10,15.
【解析】
(1)根据22=4,24=16,26=32写成对数式即可;
(2)设logaM=x,logaN=y,根据对数的定义可表示为指数式为:ax=M,ay=N,据此计算即可;
(3)由loga3=5,得a5=3,再根据同底数幂的乘法法则计算即可.
(1)∵22=4,24=16,26=32,
∴log24=2;log216=4;log264=6.
故答案为:2;4;6;
(2)设logaM=x,logaN=y,
则ax=M,ay=N,∴MN=axay=ax+y,
根据对数的定义,x+y=logaMN,
即logaM+logaN=logaMN.
故答案为:logaMN.
(3)由loga3=5,得a5=3.
∵9=3×3=a5a5=a10,27=3×3×3=a5a5a5=a15,
∴根据对数的定义,loga9=10,loga27=15.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=x﹣2与两坐标轴分别交于点A,C,交y=
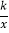 (x>0)于点P,PQ⊥x轴于点Q,CQ=1.
(x>0)于点P,PQ⊥x轴于点Q,CQ=1.(1)求反比例函数解析式;
(2)平行于y轴的直线x=m分别交y=x﹣2,y=
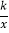 (x>0)于点D,B(B在线段AP上方),若S△BOD=2,求m值.
(x>0)于点D,B(B在线段AP上方),若S△BOD=2,求m值.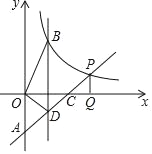
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填写下表,观察被开方数
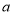 的小数点与算术平方根
的小数点与算术平方根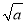 的小数点的移动规律:
的小数点的移动规律: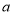
0.0016
0.16
16
1600
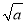
0.04
0.4
(2)根据你发现的规律填空:
①已知
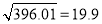 ,则
,则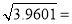 .
.②已知
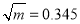 ,
,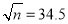 ,则
,则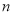 是
是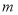 的 倍.
的 倍. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“奇巧数”,如
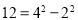 ,
, ,
,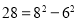 ,,因此
,,因此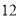 ,
,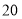 ,
,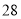 都是奇巧数.
都是奇巧数.(1)
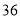 ,
,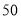 是奇巧数吗?为什么?
是奇巧数吗?为什么?(2)设两个连续偶数为
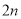 ,
,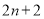 (其中
(其中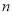 为正整数),由这两个连续偶数构造的奇巧数是4的倍数吗?为什么?
为正整数),由这两个连续偶数构造的奇巧数是4的倍数吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】小明根据学习函数的经验,对函数y=x+
 的图象与性质进行了探究.
的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
(1)函数y=x+
 的自变量x的取值范围是_____.
的自变量x的取值范围是_____.(2)下表列出了y与x的几组对应值,请写出m,n的值:m=_____,n=_____;
x
…
﹣3
﹣2
﹣1
﹣

﹣



1
2
3
4
…
y
…
﹣

﹣

﹣2
﹣

﹣

m

2

n

…
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)结合函数的图象,请完成:
①当y=﹣
 时,x=_____.
时,x=_____.②写出该函数的一条性质_____.
③若方程x+
 =t有两个不相等的实数根,则t的取值范围是_____.
=t有两个不相等的实数根,则t的取值范围是_____.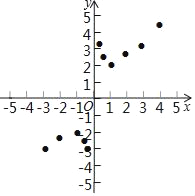
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,正方形ABCD是由两个长为a、宽为b的长方形和两个边长分别为a、b的正方形拼成的.
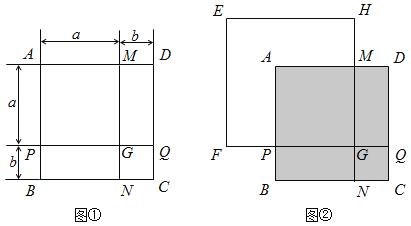
(1)利用正方形ABCD面积的不同表示方法,直接写出
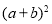 、
、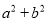 、ab之间的关系式,这个关系式是 ;
、ab之间的关系式,这个关系式是 ;(2)若m满足
 ,请利用(1)中的数量关系,求
,请利用(1)中的数量关系,求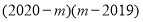 的值;
的值;(3)若将正方形EFGH的边
 、
、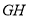 分别与图①中的PG、MG重叠,如图②所示,已知PF=8,NH=32,求图中阴影部分的面积(结果必须是一个具体数值).
分别与图①中的PG、MG重叠,如图②所示,已知PF=8,NH=32,求图中阴影部分的面积(结果必须是一个具体数值). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=
 (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤
 的解集.
的解集.
相关试题

