【题目】如图,某建筑物BC上有一旗杆AB,小明在与BC相距12m的F处,由E点观测到旗杆顶部A的仰角为52°、底部B的仰角为45°,小明的观测点与地面的距离EF为1.6m.
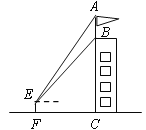
(1)求建筑物BC的高度;
(2)求旗杆AB的高度.
(结果精确到0.1m.参考数据:![]() ≈1.41,sin52°≈0.79,tan52°≈1.28)
≈1.41,sin52°≈0.79,tan52°≈1.28)
参考答案:
【答案】(1)建筑物BC的高度为13.6m.(2)旗杆AB的高度约为3.4m.
【解析】
试题分析:(1)先过点E作ED⊥BC于D,由已知底部B的仰角为45°得BD=ED=FC=12,DC=EF=1.6,从而求出BC.
(2)由已知由E点观测到旗杆顶部A的仰角为52°可求出AD,则AB=AD-BD.
试题解析:(1)过点E作ED⊥BC于D,
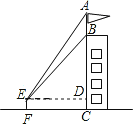
根据题意得:EF⊥FC,ED∥FC,
∴四边形CDEF是矩形,
已知底部B的仰角为45°即∠BED=45°,
∴∠EBD=45°,
∴BD=ED=FC=12,
∴BC=BD+DC=BD+EF=12+1.6=13.6,
答:建筑物BC的高度为13.6m.
(2)已知由E点观测到旗杆顶部A的仰角为52°,即∠AED=52°,
∴AD=ED![]() tan52°
tan52°
≈12×1.28≈15.4,
∴AB=AD-BD=15.4-12=3.4.
答:旗杆AB的高度约为3.4m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】能判断一个平行四边形是矩形的条件是( )
A.两条对角线互相平分B.一组邻边相等
C.两条对角线互相垂直D.两条对角线相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道平方运算和开方运算是互逆运算,如:
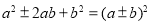 ,那么
,那么 ,那么如何将双重二次根式
,那么如何将双重二次根式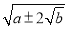
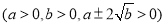 化简呢?如能找到两个数
化简呢?如能找到两个数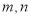
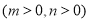 ,使得
,使得 即
即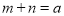 ,且使
,且使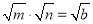 即
即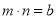 ,
,那么
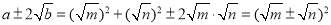
 ,双重二次根式得以化简;
,双重二次根式得以化简;例如化简:
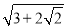 ;
; 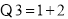 且
且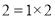 ,
,
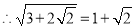
由此对于任意一个二次根式只要可以将其化成
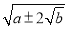 的形式,且能找到
的形式,且能找到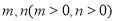 使得
使得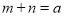 ,且
,且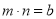 ,那么这个双重二次根式一定可以化简为一个二次根式.请同学们通过阅读上述材料,完成下列问题:
,那么这个双重二次根式一定可以化简为一个二次根式.请同学们通过阅读上述材料,完成下列问题:(1)填空:
 _________________;
_________________; 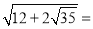 __________________;
__________________; (2)化简:①
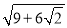 ②
②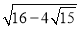
(3)计算:
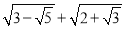
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③
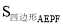 =
=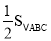 ; ④BE+CF=EF.⑤当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合).上述结论中始终正确的有 (填序号).
; ④BE+CF=EF.⑤当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合).上述结论中始终正确的有 (填序号).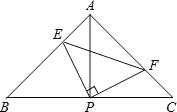
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数 y x 3 ,下列结论正确的是( )
A.当 x 4 时, y 0B.它的图象经过第一、二、三象限
C.它的图象必经过点(-1, 3)D.y 的值随 x 值的增大而增大
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c和y=max2+mbx+mc,其中a,b,c,m均为正数,且m≠1.则关于这两条抛物线,下列判断正确的是( )
A. 顶点的纵坐标相同 B. 对称轴相同
C. 与y轴的交点相同 D. 其中一条经过平移可以与另一条重合
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式a2﹣4a分解因式为 .
相关试题

