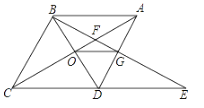
【题目】如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE,分别交AC、AD于点F、G,连接OG,则下列结论:①OG=![]() AB;②图中与△EGD全等的三角形共有5个;③以点A、B、D、E为项点的四边形是菱形;④S四边形ODGF=S△ABF.其中正确的结论是( )
AB;②图中与△EGD全等的三角形共有5个;③以点A、B、D、E为项点的四边形是菱形;④S四边形ODGF=S△ABF.其中正确的结论是( )
A. ①③B. ①③④C. ①②③D. ②②④
参考答案:
【答案】A
【解析】
由AAS证明△ABG≌△DEG,得出AG=DG,证出OG是△ACD的中位线,得出OG=![]() CD=
CD=![]() AB,①正确;先证明四边形ABDE是平行四边形,证出△ABD、△BCD是等边三角形,得出AB=BD=AD,因此OD=AG,得出四边形ABDE是菱形,③正确;由菱形的性质得得出△ABG≌△BDG≌△DEG,由SAS证明△ABG≌△DCO,得出△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,得出②不正确;证出OG是△ABD的中位线,得出OG//AB,OG=
AB,①正确;先证明四边形ABDE是平行四边形,证出△ABD、△BCD是等边三角形,得出AB=BD=AD,因此OD=AG,得出四边形ABDE是菱形,③正确;由菱形的性质得得出△ABG≌△BDG≌△DEG,由SAS证明△ABG≌△DCO,得出△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,得出②不正确;证出OG是△ABD的中位线,得出OG//AB,OG=![]() AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形ODGF=S△ABF;④不正确;即可得出结果.
AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形ODGF=S△ABF;④不正确;即可得出结果.
解:四边形ABCD是菱形,

在△ABG和△DEG中,
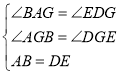
∴△ABG≌△DEG(AAS),
∴.AG=DG,
∴OG是△ACD的中位线,
∴OG=![]() CD=
CD=![]() AB,①正确;
AB,①正确;
∵AB//CE,AB=DE,
∴四边形ABDE是平行四边形,
∴∠BCD=∠BAD=60°,
∴△ABD、△BCD是等边三角形,
∴AB=BD=AD,∠ODC=60°,
∴OD=AG,四边形ABDE是菱形,③正确;
∴AD⊥BE,
由菱形的性质得:△ABG≌△BDG≌△DEG,
在△ABG和△DCO中,
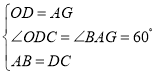
∴△ABG≌△DCO
∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,则②不正确。
∵OB=OD,AG=DG,
∴OG是△ABD的中位线,
∴OG∥AB,OG=![]() AB,
AB,
∴△GOD∽△ABD,△ABF∽△OGF,
∴△GOD的面积=![]() △ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
△ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
∴△AFG的面积=△OGF的面积的2倍,
又∵△GOD的面积=△AOG的面积=△BOG的面积,
∴ S四边形ODGF=S△ABF;④不正确;
故答案为:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 、
、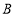 两地相距
两地相距 ,
, 地在
地在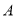 、
、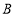 两地之间.一辆轿车以
两地之间.一辆轿车以 的速度从
的速度从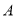 地出发匀速行驶,前往
地出发匀速行驶,前往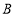 地.同时,一辆货车以
地.同时,一辆货车以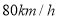 的速度从
的速度从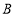 地出发,匀速行驶,前往
地出发,匀速行驶,前往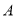 地.
地.(1)当两车相遇时,求轿车行驶的时间;
(2)当两车相距
 时,求轿车行驶的时间.
时,求轿车行驶的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O为正方形ABCD的外接圆,E为弧BC上一点,AF⊥DE于F,连OF、OD.
(1)求证:AF=EF;
(2)若
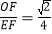 ,求sin∠DOF的值.
,求sin∠DOF的值.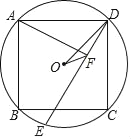
-
科目: 来源: 题型:
查看答案和解析>>【题目】等边△ABC的边长为6,点O是三边垂直平分线的交点,∠FOG=120°,∠FOG的两边OF,OG分别交AB,BC与点D,E,∠FOG绕点O顺时针旋转时,下列四个结论正确的是( )
①OD=OE;②
 ;③
;③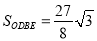 ;④△BDE的周长最小值为9.
;④△BDE的周长最小值为9.A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】小图暑假期间参加社会实践活动,从某批发市场以每个a元的价格购进50个手机充电宝,然后每个加价b元到市场出售.
(1)求全部售出50个手机充电宝的总销售额为多少元(结果用含a,b的式子表示)?
(2)由于开学临近,小丽在成功售出30个充电宝后,决定将剩余充电宝按售价8折出售,并很快全部售完.
①她的总销售额是多少元?
②相比不采取降价销售,她将比实际销售多盈利多少元(结果用含a、b的式子表示)
③若a=2b,小丽实际销售完这批充电宝的利润率为 (利润率=利润÷进价100%).
-
科目: 来源: 题型:
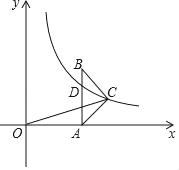
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,AB⊥x轴于A,反比例函数y=
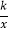 (x>0)的图象经过点C,交AB于点D,已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D,已知AB=4,BC= .
.(1)若OA=4,求k的值.
(2)连接OC,若AD=AC,求CO的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠ADC=90°,DE⊥BC于E,连AE,FE⊥AE交CD于点F.
(1)求证:△AED∽△FEC;
(2)若AB=2
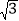 ,求DF的值;
,求DF的值;
相关试题

