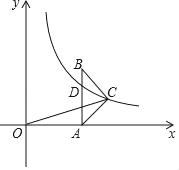
【题目】如图,在△ABC中,AC=BC,AB⊥x轴于A,反比例函数y=![]() (x>0)的图象经过点C,交AB于点D,已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D,已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值.
(2)连接OC,若AD=AC,求CO的长.
参考答案:
【答案】(1)k=11;(2)![]()
【解析】试题分析:(1)利用等腰三角形的性质得出AE,BE的长,再利用勾股定理得出OA的长,得出C点坐标即可得出答案;
(2)首先表示出D,C点坐标进而利用反比例函数图象上的性质求出C点坐标,再利用勾股定理得出CO的长.
试题解析:解:(1)作CE⊥AB,垂足为E.∵AC=BC,AB=4,∴AE=BE=2.
在Rt△BCE中,BC=![]() ,BE=2,∴CE=
,BE=2,∴CE=![]() .∵OA=4,∴C点的坐标为:(
.∵OA=4,∴C点的坐标为:(![]() ,2).∵点C在y=
,2).∵点C在y=![]() (x>0)的图象上,∴k=11;
(x>0)的图象上,∴k=11;
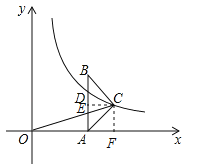
(2)设A点的坐标为(m,0).∵BD=BC=![]() ,∴AD=
,∴AD=![]() ,∴D,C两点的坐标分别为:(m,
,∴D,C两点的坐标分别为:(m,![]() ),(m+
),(m+![]() ,2).
,2).
∵点C,D都在y=![]() (x>0)的图象上,∴
(x>0)的图象上,∴![]() m=2(m+
m=2(m+![]() ),∴m=6,∴C点的坐标为:(
),∴m=6,∴C点的坐标为:(![]() ,2),作CF⊥x轴,垂足为F,∴OF=
,2),作CF⊥x轴,垂足为F,∴OF=![]() ,CF=2.在Rt△OFC中,OC2=OF2+CF2,∴OC=
,CF=2.在Rt△OFC中,OC2=OF2+CF2,∴OC=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等边△ABC的边长为6,点O是三边垂直平分线的交点,∠FOG=120°,∠FOG的两边OF,OG分别交AB,BC与点D,E,∠FOG绕点O顺时针旋转时,下列四个结论正确的是( )
①OD=OE;②
 ;③
;③ ;④△BDE的周长最小值为9.
;④△BDE的周长最小值为9.A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE,分别交AC、AD于点F、G,连接OG,则下列结论:①OG=
 AB;②图中与△EGD全等的三角形共有5个;③以点A、B、D、E为项点的四边形是菱形;④S四边形ODGF=S△ABF.其中正确的结论是( )
AB;②图中与△EGD全等的三角形共有5个;③以点A、B、D、E为项点的四边形是菱形;④S四边形ODGF=S△ABF.其中正确的结论是( )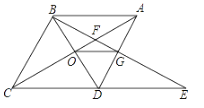
A. ①③B. ①③④C. ①②③D. ②②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】小图暑假期间参加社会实践活动,从某批发市场以每个a元的价格购进50个手机充电宝,然后每个加价b元到市场出售.
(1)求全部售出50个手机充电宝的总销售额为多少元(结果用含a,b的式子表示)?
(2)由于开学临近,小丽在成功售出30个充电宝后,决定将剩余充电宝按售价8折出售,并很快全部售完.
①她的总销售额是多少元?
②相比不采取降价销售,她将比实际销售多盈利多少元(结果用含a、b的式子表示)
③若a=2b,小丽实际销售完这批充电宝的利润率为 (利润率=利润÷进价100%).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠ADC=90°,DE⊥BC于E,连AE,FE⊥AE交CD于点F.
(1)求证:△AED∽△FEC;
(2)若AB=2
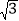 ,求DF的值;
,求DF的值;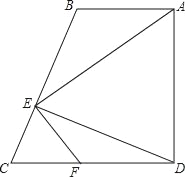
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB∶BC=3∶2,∠DAB=60°,E在AB上,且AE∶EB=1∶2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP∶DQ等于

A.3∶4 B.
 ∶
∶ C.
C. ∶
∶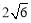 D.
D.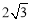 ∶
∶
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,长方形
 的顶点
的顶点 在坐标原点,顶点
在坐标原点,顶点 分别在
分别在 轴,
轴, 轴的正半轴上,
轴的正半轴上, ,
, 为边
为边 的中点,
的中点, 是边
是边 上的一个动点,当
上的一个动点,当 的周长最小时,点
的周长最小时,点 的坐标为_________.
的坐标为_________.
相关试题

