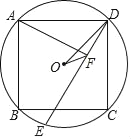
【题目】如图,⊙O为正方形ABCD的外接圆,E为弧BC上一点,AF⊥DE于F,连OF、OD.
(1)求证:AF=EF;
(2)若![]() ,求sin∠DOF的值.
,求sin∠DOF的值.
参考答案:
【答案】(1)见解析;(2)![]()
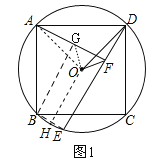
【解析】试题分析:(1)如图,过B作BG⊥AF于G,连接BE、OB,只要证明四边形BGEF是矩形,△ABG≌△DAF即可解决问题;
(2)作OH⊥BE于H,连接AO,GO.首先证明OH垂直平分线段FG,再证明∠DOF=∠DAF,△FOG是等腰直角三角形即可解决问题;
试题解析:证明:(1)如图,过B作BG⊥AF于G,连接BE、OB.∵AF⊥DE,∴∠AGB=∠AFD=90°,∴∠BAF+∠ABG=90°.∵四边形ABCD是正方形,∴BD为⊙O的直径,AD=AB,∠BAD=90°,∴∠DAF+∠BAF=90°,∠BED=90°,∴∠ABG=∠DAF,∴△ABG≌△DAF,∴BG=AF.∵∠BED=∠BGF=∠AFE=90°,∴四边形GBEF是矩形,∴EF=BG,∴AF=EF;
(2)作OH⊥BE于H,连接AO,GO.
∵OH⊥BE,∴BH=HE,∴OH垂直平分线段BE.∵四边形GBEF是矩形,∴BE=GF,BE∥GF,∴OH垂直平分线段FG,∴OG=OF.∵∠AOD=∠AFD=90°,∴A、D、F、O四点共圆,∴∠DOF=∠DAF,∠OFG=∠ADO=45°,∴△FOG是等腰直角三角形,∴FG=![]() OF.∵EF=BG=AF=2
OF.∵EF=BG=AF=2![]() OF,∴AF=2FG,AG=FG=DF,设DF=a,则AF=2a,AD=
OF,∴AF=2FG,AG=FG=DF,设DF=a,则AF=2a,AD=![]() a,∴sin∠DOF=sin∠DAF=
a,∴sin∠DOF=sin∠DAF=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若甲、乙两人同时从某地出发,沿着同一个方向行走到同一个目的地,其中甲一半的路程以a(km/h)的速度行走,另一半的路程以b(km/h)的速度行走;乙一半的时间以a(km/h)的速度行走,另一半的时间以b(km/h)的速度行走(a≠b),则先到达目的地的是( )
A. 甲B. 乙
C. 同时到达D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 、
、 两地相距
两地相距 ,
, 地在
地在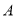 、
、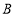 两地之间.一辆轿车以
两地之间.一辆轿车以 的速度从
的速度从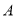 地出发匀速行驶,前往
地出发匀速行驶,前往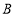 地.同时,一辆货车以
地.同时,一辆货车以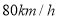 的速度从
的速度从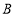 地出发,匀速行驶,前往
地出发,匀速行驶,前往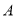 地.
地.(1)当两车相遇时,求轿车行驶的时间;
(2)当两车相距
 时,求轿车行驶的时间.
时,求轿车行驶的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】等边△ABC的边长为6,点O是三边垂直平分线的交点,∠FOG=120°,∠FOG的两边OF,OG分别交AB,BC与点D,E,∠FOG绕点O顺时针旋转时,下列四个结论正确的是( )
①OD=OE;②
 ;③
;③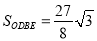 ;④△BDE的周长最小值为9.
;④△BDE的周长最小值为9.A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE,分别交AC、AD于点F、G,连接OG,则下列结论:①OG=
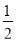 AB;②图中与△EGD全等的三角形共有5个;③以点A、B、D、E为项点的四边形是菱形;④S四边形ODGF=S△ABF.其中正确的结论是( )
AB;②图中与△EGD全等的三角形共有5个;③以点A、B、D、E为项点的四边形是菱形;④S四边形ODGF=S△ABF.其中正确的结论是( )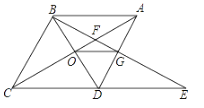
A. ①③B. ①③④C. ①②③D. ②②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】小图暑假期间参加社会实践活动,从某批发市场以每个a元的价格购进50个手机充电宝,然后每个加价b元到市场出售.
(1)求全部售出50个手机充电宝的总销售额为多少元(结果用含a,b的式子表示)?
(2)由于开学临近,小丽在成功售出30个充电宝后,决定将剩余充电宝按售价8折出售,并很快全部售完.
①她的总销售额是多少元?
②相比不采取降价销售,她将比实际销售多盈利多少元(结果用含a、b的式子表示)
③若a=2b,小丽实际销售完这批充电宝的利润率为 (利润率=利润÷进价100%).
相关试题

