【题目】某公司为了宣传一种新产品,在某地先后举行![]() 场产品促销会,已知该产品每台成本为
场产品促销会,已知该产品每台成本为![]() 万元,设第
万元,设第![]() 场产品的销售量为
场产品的销售量为![]() (台),在销售过程中获得以下信息:
(台),在销售过程中获得以下信息:
信息1:已知第一场销售产品![]() 台,然后每增加一场,产品就少卖出
台,然后每增加一场,产品就少卖出![]() 台;
台;
信息2:产品的每场销售单价![]() (万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次
(万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次![]() 成正比,第21场--第40场浮动价与销售场次
成正比,第21场--第40场浮动价与销售场次![]() 成反比,经过统计,得到如下数据:
成反比,经过统计,得到如下数据:
| 3 | 10 | 25 |
| 10.6 | 12 | 14.2 |
(1)求![]() 与
与![]() 之间满足的函数关系式;
之间满足的函数关系式;
(2)当产品销售单价为13万元时,求销售场次是第几场?
(3)在这![]() 场产品促销会中,哪一场获得的利润最大,最大利润是多少?
场产品促销会中,哪一场获得的利润最大,最大利润是多少?
参考答案:
【答案】(1)![]() (2)当产品销售单价为
(2)当产品销售单价为![]() 万元时,销售场次是第
万元时,销售场次是第![]() 场和第
场和第![]() 场;(3)在这
场;(3)在这![]() 场产品促销会中,第
场产品促销会中,第![]() 场获得的利润最大,最大利润为
场获得的利润最大,最大利润为![]() 万元.
万元.
【解析】
![]() 根据每增加一场,产品就少卖出一台,即可列出关系式;
根据每增加一场,产品就少卖出一台,即可列出关系式;
![]() 分别求出第1场--第20场与第21场--第40场的函数关系式,令函数值等于13万元,即可求出销售场次;
分别求出第1场--第20场与第21场--第40场的函数关系式,令函数值等于13万元,即可求出销售场次;
![]() 根据第1场--第20场与第21场--第40场的函数关系式,判断利润随场次的变化情况,在根据二次函数与反比例函数的性质求得最大值即可.
根据第1场--第20场与第21场--第40场的函数关系式,判断利润随场次的变化情况,在根据二次函数与反比例函数的性质求得最大值即可.
![]() 依题意得:
依题意得:![]() ,其中
,其中![]() 为正整数,且1
为正整数,且1![]() ;
;
![]() 设基本价为
设基本价为![]() ,第
,第![]() 场--第
场--第![]() 场,设
场,设![]() 与
与![]() 的函数关系式为
的函数关系式为![]() ,
,
依题意得![]()
解得
![]() .
.
第![]() 场----第
场----第![]() 场,设
场,设![]() 与
与![]() 的函数关系式为
的函数关系式为![]() ,
,
当![]() 时,有
时,有![]() ,解得
,解得![]() ,
,
![]() .
.
当![]() 时,令
时,令![]() ,解得
,解得 ![]() .
.
当![]() 时,
时,![]() ,解得
,解得![]() .
.
经检验:![]() 或
或![]() 都是相应方程的根.
都是相应方程的根.
∴当产品销售单价为![]() 万元时,销售场次是第
万元时,销售场次是第![]() 场和第
场和第![]() 场.
场.
![]() 设每场获得的利润为
设每场获得的利润为![]() (万元),
(万元),
当![]() 时,
时,![]() ,
,
![]() 随
随![]() 的增大而增大,
的增大而增大,
![]() 当
当![]() 时,
时,![]() 最大,最大利润为
最大,最大利润为![]() 元.
元.
当![]() 时,
时,![]() ,
,
![]() 随
随![]() 的增大而减小,
的增大而减小,
![]() 当
当![]() 时,
时,![]() 最大,最大利润为
最大,最大利润为![]() 万元,
万元,
![]() ,
,
![]() 在这
在这![]() 场产品促销会中,第
场产品促销会中,第![]() 场获得的利润最大,最大利润为
场获得的利润最大,最大利润为![]() 万元.
万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
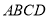 中,点
中,点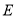 是边
是边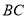 上一点(不与点
上一点(不与点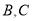 重合),点
重合),点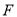 是
是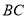 延长线上一点,且
延长线上一点,且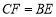 ,连接
,连接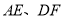 .
.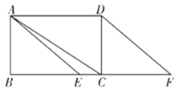
(1)求证:
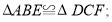
(2)连接
 ,其中
,其中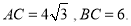
①当四边形
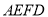 是菱形时,求线段
是菱形时,求线段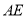 与线段
与线段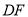 之间的距离;
之间的距离;②若点
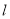 是
是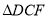 的内心,连接
的内心,连接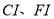 ,直接写出
,直接写出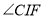 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,我们定义:横坐标与纵坐标均为整数的点为整点如图,已知双曲线
 经过点
经过点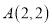 ,记双曲线与两坐标轴之间的部分为
,记双曲线与两坐标轴之间的部分为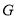 (不含双曲线与坐标轴).
(不含双曲线与坐标轴).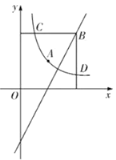
(1)求
 的值;
的值;(2)求
 内整点的个数;
内整点的个数;(3)设点
 在直线
在直线 上,过点
上,过点 分别作平行于
分别作平行于 轴
轴 轴的直线,交双曲线
轴的直线,交双曲线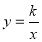
 于点
于点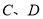 ,记线段
,记线段 、双曲线所围成的区域为
、双曲线所围成的区域为 ,若
,若 内部(不包括边界)不超过
内部(不包括边界)不超过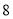 个整点,求
个整点,求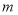 的取值范围.
的取值范围. -
科目: 来源: 题型:
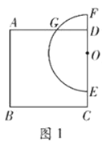
查看答案和解析>>【题目】如图1,在正方形
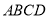 中,
中,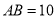 ,点
,点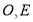 在边
在边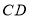 上,且
上,且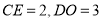 ,以点
,以点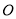 为圆心,
为圆心,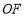 为半径在其左侧作半圆
为半径在其左侧作半圆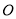 ,分别交
,分别交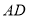 )于点
)于点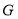 ,交
,交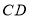 的延长线于点
的延长线于点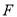 .
.
(1)
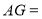 ;
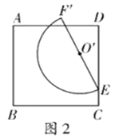
;(2)如图2,将半圆
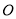 绕点
绕点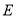 逆时针旋转
逆时针旋转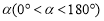 ,点
,点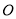 的对应点为
的对应点为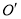 ,点
,点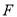 的对应点为
的对应点为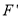 ;设
;设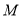 为半圆
为半圆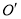 上一点.
上一点.①当点
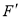 落在
落在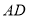 边上时,求点
边上时,求点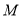 与线段
与线段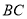 之间的最短距离;
之间的最短距离;②当半圆
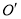 交
交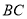 于
于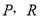 两点时,若
两点时,若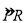 的长为
的长为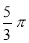 ,求此时半圆
,求此时半圆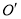 与正方形
与正方形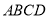 重叠部分的面积;
重叠部分的面积;③当半圆
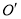 与正方形
与正方形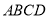 的边相切时,设切点为
的边相切时,设切点为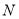 ,直接写出
,直接写出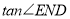 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】
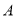 地和
地和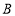 地之间有一条笔直的公路,一天,甲车从
地之间有一条笔直的公路,一天,甲车从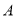 地去
地去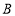 地,乙车从
地,乙车从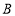 地去
地去 地,乙先出发,若甲、乙之间的距离为
地,乙先出发,若甲、乙之间的距离为 千米,行驶时间为
千米,行驶时间为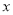 小时,
小时, 与
与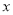 之间的函数关系如图所示,则下列说法错误的是 ( )
之间的函数关系如图所示,则下列说法错误的是 ( )
A.
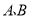 两地间距离为100千米B.甲车的速度是80千米/时
两地间距离为100千米B.甲车的速度是80千米/时C.甲到
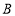 地比乙车到
地比乙车到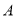 地早
地早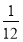 小时D.甲出发0.5小时后与乙车相遇
小时D.甲出发0.5小时后与乙车相遇 -
科目: 来源: 题型:
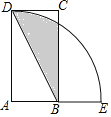
查看答案和解析>>【题目】如图,四边形ABCD为矩形,以A为圆心,AD为半径的弧交AB的延长线于点E,连接BD,若AD=2AB=4,则图中阴影部分的面积为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,正方形
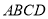 的位置如图所示,点
的位置如图所示,点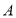 的坐标为
的坐标为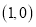 ,点
,点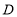 的坐标为
的坐标为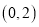 ,延长
,延长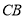 交
交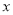 轴于点
轴于点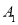 ,作正方形
,作正方形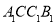 ;延长
;延长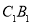 交
交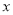 轴于点
轴于点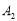 ,作正方形
,作正方形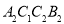 ;…,按照这样的规律作正方形,则点
;…,按照这样的规律作正方形,则点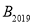 的纵坐标为__________.
的纵坐标为__________.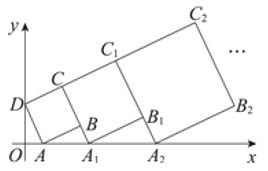
相关试题

