【题目】如图1,在正方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 为半径在其左侧作半圆
为半径在其左侧作半圆![]() ,分别交
,分别交![]() )于点
)于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
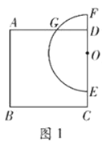
(1)![]() ;
;
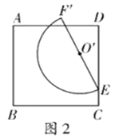
(2)如图2,将半圆![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,点
,点![]() 的对应点为
的对应点为![]() ,点
,点![]() 的对应点为
的对应点为![]() ;设
;设![]() 为半圆
为半圆![]() 上一点.
上一点.
①当点![]() 落在
落在![]() 边上时,求点
边上时,求点![]() 与线段
与线段![]() 之间的最短距离;
之间的最短距离;
②当半圆![]() 交
交![]() 于
于![]() 两点时,若
两点时,若![]() 的长为
的长为![]() ,求此时半圆
,求此时半圆![]() 与正方形
与正方形![]() 重叠部分的面积;
重叠部分的面积;
③当半圆![]() 与正方形
与正方形![]() 的边相切时,设切点为
的边相切时,设切点为![]() ,直接写出
,直接写出![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)①点
;(2)①点![]() 到
到![]() 的最短距离为
的最短距离为![]() ,②此时半圆
,②此时半圆![]() 与正方形
与正方形![]() 重叠部分的面积为
重叠部分的面积为![]() ;③
;③![]()
【解析】
(1)连接GO,根据已知条件,在△DGO中利用勾股定理即可求解;
(2)①如图,过点O'作O'H⊥BC,根据三点共线及垂线段最短可得此时MH即为点M到BC的最短距离,根据已知求得HQ、O'Q、O'M,而MH=HQ- O'Q- O'M即可求得;
②如图,根据![]() 的长可以求出∠PO'R=60°,此时半圆
的长可以求出∠PO'R=60°,此时半圆![]() 与正方形
与正方形![]() 重叠部分的面积为
重叠部分的面积为![]() ,即可求得答案;
,即可求得答案;
③当半圆![]() 与正方形
与正方形![]() 的边相切时有三种情况,分别作图,
的边相切时有三种情况,分别作图,
第一种情况:当半圆![]() 与BC边相切时,连接O'N,,过点E作ET⊥O'N于T,连接EN,过点E作EK⊥DN于K,再依据勾股定理以及等面积法求得EK、NK的值,进而可以求得
与BC边相切时,连接O'N,,过点E作ET⊥O'N于T,连接EN,过点E作EK⊥DN于K,再依据勾股定理以及等面积法求得EK、NK的值,进而可以求得![]() ;
;
第二种情况:当半圆![]() 与AB边相切时,连接DN,如图,根据已知条件可以判断四边形ANED是矩形,进而可以求得
与AB边相切时,连接DN,如图,根据已知条件可以判断四边形ANED是矩形,进而可以求得![]() ;
;
第三种情况:当半圆O'与CD相切于点N时,此时点N与点E重合,![]() 不存在.
不存在.
(1)连接GO,如图:
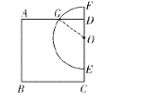
∵四边形ABCD是正方形,AB=10,
∴DC=AD=10,∠ODG=90°,
∵CE=2,DO=3,
∴OG=OE=DC-DO-CE=10-3-2=5,
∴DG=![]() =
=![]() 4,
4,
∴AG=AD-DG=10-4=6.
故答案为6.
(2)①如图,过点O'作O'H⊥BC于点H,交半圆O'于点M,反向延长HO交AD于
点Q,则∠QHC=90°,
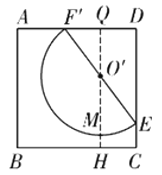
根据三点共线及垂线段最短可得此时点M到BC的距离最短,
∵∠C=∠D=∠QHC=90°,
∴四边形QHCD是矩形,
∴HQ=CD=10,HQ//CD,
∵点O'是EF'的中点, 点Q是DF'的中点,
∵DE=8,
∴O'Q=![]() DE=4,
DE=4,
∴O'H=10-4=6,
∵CE=2,DO=3,
∴OE=10-2-3=5,即半圆O的半径为5,
∴MH=HQ- O'Q- O'M=10-4-5=1,
即点M到BC的最短距离为1.
②由①可知半圆O的半径为5,如图
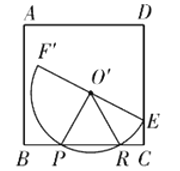
设∠PO'R的度数为![]() ,
,
由题意得: ![]() 的长为=
的长为=![]() ,
,
∴∠PO'R=60°,
∴∠F'O'P+∠EO'R=120°,
![]() ,
,
∵O'R=P O',
∴△O'RP是等边三角形,
∴![]() .
.
∴此时半圆O'与正方形![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
③第一种情况:当半圆O'与BC相切于N时,连接O'N,,过点E作ET⊥O'N于T,连接EN,
则TN=EC=2,如图:
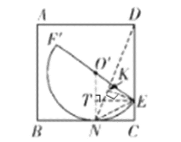
∵ON=O'E=5,
∴O'T=ON-TN=5-2=3
∴ CN2=TE2= O'E2- O'T2
∴ CN=TE=![]() =4,
=4,
∴![]() =
=![]() ,
,
![]() =
=![]() ,
,
过点E作EK⊥DN于K,
∵![]() =
=![]() EK
EK![]() DN=
DN=![]() DE
DE![]() CN,
CN,
∴EK=![]() =
=![]() =
=![]() ,
,
∵![]() =
=![]() =
=![]() ,
,
∴![]() ,
,
∴NK=![]() ,
,
∴![]() =
=![]() =
=![]() ;
;
第二种情况:当半圆O'与AB相切于点N时,连接DN,如图
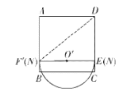
∵EN⊥AB,
∴四边形ANED是矩形,
∴![]() =
=![]() =
=![]() ,
,
第三种情况:当半圆O'与CD相切于点N时,此时点N与点E重合,![]() 不存在,
不存在,
综上所述,![]() 的值为
的值为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在抗击新型冠状病毒肺炎战役中,某市党员积极响应国家号召参加志愿者活动,为人民服务,现随机抽查部分党员一个月来参加志愿者活动的次数,并绘制成如下尚不完整的条形统计图(图1)和扇形统计图(图2).
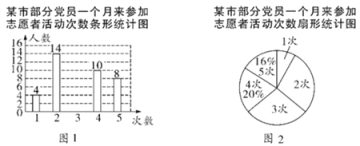
(1) “
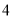 次”所在扇形的圆心角度数是 ,请补全 条形统计图;
次”所在扇形的圆心角度数是 ,请补全 条形统计图;(2)若从抽在的党员中随机选择一位接受媒体的采访,求该党员一个月来参加志愿者活动次数不少于
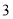 次的概率;
次的概率;(3)设随机抽查的党员一个月来参加志愿者活动次数的中位数为
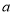 ,若去掉一部分党员参加志愿者活动的次数后,得到一组新数据的众数为
,若去掉一部分党员参加志愿者活动的次数后,得到一组新数据的众数为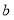 ,当
,当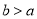 时,求最少去掉了几名党员参加志愿者活动的次数.
时,求最少去掉了几名党员参加志愿者活动的次数. -
科目: 来源: 题型:
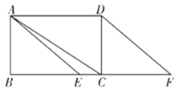
查看答案和解析>>【题目】如图,在矩形
 中,点
中,点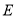 是边
是边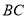 上一点(不与点
上一点(不与点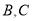 重合),点
重合),点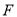 是
是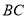 延长线上一点,且
延长线上一点,且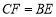 ,连接
,连接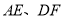 .
.
(1)求证:
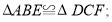
(2)连接
 ,其中
,其中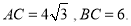
①当四边形
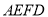 是菱形时,求线段
是菱形时,求线段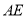 与线段
与线段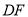 之间的距离;
之间的距离;②若点
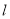 是
是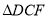 的内心,连接
的内心,连接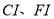 ,直接写出
,直接写出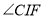 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,我们定义:横坐标与纵坐标均为整数的点为整点如图,已知双曲线
 经过点
经过点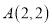 ,记双曲线与两坐标轴之间的部分为
,记双曲线与两坐标轴之间的部分为 (不含双曲线与坐标轴).
(不含双曲线与坐标轴).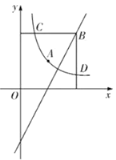
(1)求
 的值;
的值;(2)求
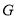 内整点的个数;
内整点的个数;(3)设点
 在直线
在直线 上,过点
上,过点 分别作平行于
分别作平行于 轴
轴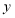 轴的直线,交双曲线
轴的直线,交双曲线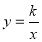
 于点
于点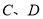 ,记线段
,记线段 、双曲线所围成的区域为
、双曲线所围成的区域为 ,若
,若 内部(不包括边界)不超过
内部(不包括边界)不超过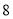 个整点,求
个整点,求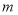 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了宣传一种新产品,在某地先后举行
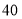 场产品促销会,已知该产品每台成本为
场产品促销会,已知该产品每台成本为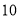 万元,设第
万元,设第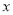 场产品的销售量为
场产品的销售量为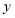 (台),在销售过程中获得以下信息:
(台),在销售过程中获得以下信息:信息1:已知第一场销售产品
 台,然后每增加一场,产品就少卖出
台,然后每增加一场,产品就少卖出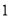 台;
台;信息2:产品的每场销售单价
 (万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次
(万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次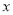 成正比,第21场--第40场浮动价与销售场次
成正比,第21场--第40场浮动价与销售场次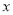 成反比,经过统计,得到如下数据:
成反比,经过统计,得到如下数据: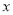 (场)
(场)3
10
25
 (万元)
(万元)10.6
12
14.2
(1)求
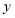 与
与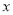 之间满足的函数关系式;
之间满足的函数关系式;(2)当产品销售单价为13万元时,求销售场次是第几场?
(3)在这
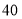 场产品促销会中,哪一场获得的利润最大,最大利润是多少?
场产品促销会中,哪一场获得的利润最大,最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】
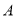 地和
地和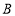 地之间有一条笔直的公路,一天,甲车从
地之间有一条笔直的公路,一天,甲车从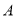 地去
地去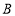 地,乙车从
地,乙车从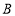 地去
地去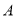 地,乙先出发,若甲、乙之间的距离为
地,乙先出发,若甲、乙之间的距离为 千米,行驶时间为
千米,行驶时间为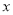 小时,
小时, 与
与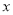 之间的函数关系如图所示,则下列说法错误的是 ( )
之间的函数关系如图所示,则下列说法错误的是 ( )
A.
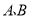 两地间距离为100千米B.甲车的速度是80千米/时
两地间距离为100千米B.甲车的速度是80千米/时C.甲到
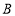 地比乙车到
地比乙车到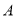 地早
地早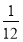 小时D.甲出发0.5小时后与乙车相遇
小时D.甲出发0.5小时后与乙车相遇 -
科目: 来源: 题型:
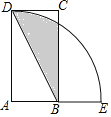
查看答案和解析>>【题目】如图,四边形ABCD为矩形,以A为圆心,AD为半径的弧交AB的延长线于点E,连接BD,若AD=2AB=4,则图中阴影部分的面积为______.
相关试题

