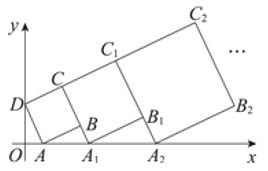
【题目】在平面直角坐标系中,正方形![]() 的位置如图所示,点
的位置如图所示,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ;延长
;延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ;…,按照这样的规律作正方形,则点
;…,按照这样的规律作正方形,则点![]() 的纵坐标为__________.
的纵坐标为__________.
参考答案:
【答案】![]()
【解析】
先根据两对对应角相等的三角形相似,证明△AOD和△A1BA相似,根据相似三角形对应边成比例可以得到AB=2A1B,所以正方形![]() 的边长等于正方形ABCD边长的
的边长等于正方形ABCD边长的![]() ,以此类推,后一个正方形的边长是前一个正方形的边长的
,以此类推,后一个正方形的边长是前一个正方形的边长的![]() ,即后一个三角形与前一个三角形的相似比为
,即后一个三角形与前一个三角形的相似比为![]() ,点B的纵坐标的值为三角形的高,因此B点的纵坐标的值依次增大
,点B的纵坐标的值为三角形的高,因此B点的纵坐标的值依次增大![]() 倍.
倍.
解:,∵四边形ABCD是正方形,
∴∠ABC=∠BAD=90°,AB=BC,
∴∠ABA1=90°,∠DAO+∠BAA1=90°,
又∵在坐标平面内,∠DAO+∠ADO=90°,
∴∠ADO=∠BAA1,
在△AOD和△A1BA中,
 ,
,
∴△AOD∽△A1BA,
∴OD:AO=AB:A1B=2,
∴BC=2A1B,
∴![]() ,
,
过点B作BE⊥x轴,
易证![]() ,
,
∴BE=OA=1,
即B点纵坐标的值为1,
∴![]() 纵坐标的值为:
纵坐标的值为:![]() ,
,
∴点![]() 的纵坐标的值为:
的纵坐标的值为:![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了宣传一种新产品,在某地先后举行
 场产品促销会,已知该产品每台成本为
场产品促销会,已知该产品每台成本为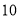 万元,设第
万元,设第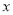 场产品的销售量为
场产品的销售量为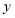 (台),在销售过程中获得以下信息:
(台),在销售过程中获得以下信息:信息1:已知第一场销售产品
 台,然后每增加一场,产品就少卖出
台,然后每增加一场,产品就少卖出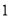 台;
台;信息2:产品的每场销售单价
 (万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次
(万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次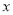 成正比,第21场--第40场浮动价与销售场次
成正比,第21场--第40场浮动价与销售场次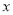 成反比,经过统计,得到如下数据:
成反比,经过统计,得到如下数据: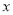 (场)
(场)3
10
25
 (万元)
(万元)10.6
12
14.2
(1)求
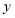 与
与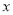 之间满足的函数关系式;
之间满足的函数关系式;(2)当产品销售单价为13万元时,求销售场次是第几场?
(3)在这
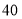 场产品促销会中,哪一场获得的利润最大,最大利润是多少?
场产品促销会中,哪一场获得的利润最大,最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】
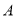 地和
地和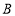 地之间有一条笔直的公路,一天,甲车从
地之间有一条笔直的公路,一天,甲车从 地去
地去 地,乙车从
地,乙车从 地去
地去 地,乙先出发,若甲、乙之间的距离为
地,乙先出发,若甲、乙之间的距离为 千米,行驶时间为
千米,行驶时间为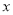 小时,
小时, 与
与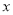 之间的函数关系如图所示,则下列说法错误的是 ( )
之间的函数关系如图所示,则下列说法错误的是 ( )
A.
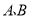 两地间距离为100千米B.甲车的速度是80千米/时
两地间距离为100千米B.甲车的速度是80千米/时C.甲到
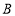 地比乙车到
地比乙车到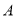 地早
地早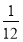 小时D.甲出发0.5小时后与乙车相遇
小时D.甲出发0.5小时后与乙车相遇 -
科目: 来源: 题型:
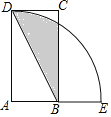
查看答案和解析>>【题目】如图,四边形ABCD为矩形,以A为圆心,AD为半径的弧交AB的延长线于点E,连接BD,若AD=2AB=4,则图中阴影部分的面积为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
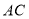 为
为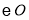 的直径,
的直径,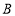 为
为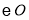 上一点,且点
上一点,且点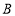 不与点
不与点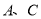 重合,点
重合,点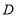 为半径
为半径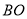 的中点,过点
的中点,过点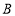 作
作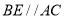 交
交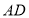 的延长线于点
的延长线于点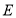 ,连接
,连接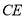 .
.(1)求证:点
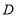 为
为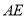 的中点;
的中点;(2)连接
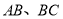 ,若
,若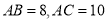 ,请直接写出
,请直接写出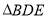 的面积.
的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们生活质量的提高,越来越多的人们关注运动与健康,近来“微信运动”逐渐被大家关注和喜爱.某兴趣小组为了了解某社区居民的“微信运动”情况,进行了随机抽样调查,对他们一日“微信运动”中的步数进行了统计,下面给出部分信息:
①
 (步数/日)
(步数/日)频数
频率
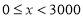
5
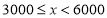
10
0.2

15
0.3
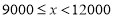
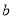
0.2
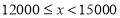
8
0.16
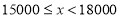
2
0.04
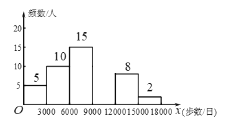
 这一组的数据为:
这一组的数据为:6000 6200 6200 6500 6600 6800 7000 7200 7200 7200 7800 8000 8300 8700 8900
根据以上信息,回答下列问题:
(1)本次被调查的居民有__________人:表中
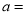 ______________,
______________,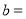 ___________;
___________;(2)补全频数分布直方图;
(3)直接写出被调查的居民在“微信运动”中步数的中位数;
(4)本社区约有5000人,用调查样本估计一日步数不低于9000步的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正比例函数
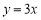 与反比例函数
与反比例函数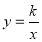 的图象相交于点
的图象相交于点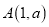 .
.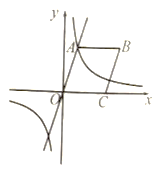
(1)填空:
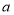 的值为_______________,
的值为_______________,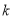 的值为_____________;
的值为_____________;(2)以点
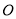 为圆心、
为圆心、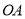 为半径画弧交
为半径画弧交 轴的正半轴于点
轴的正半轴于点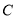 ,以
,以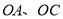 为邻边作平行四边形
为邻边作平行四边形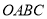 ,求点
,求点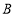 的坐标;
的坐标;(3)观察上述反比例函数
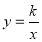 的图象,当
的图象,当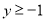 时,请直接写出自变量
时,请直接写出自变量 的取值范围.
的取值范围.
相关试题

