【题目】已知关于x的一元二次方程x2﹣(m﹣3)x﹣m=0
(1)求证:方程有两个不相等的实数根;
(2)如果方程的两实根为x1、x2 , 且x12+x22﹣x1x2=7,求m的值.
参考答案:
【答案】
(1)证明:∵x2﹣(m﹣3)x﹣m=0,
∴△=[﹣(m﹣3)]2﹣4×1×(﹣m)=m2﹣2m+9=(m﹣1)2+8>0,
∴方程有两个不相等的实数根
(2)解:∵x2﹣(m﹣3)x﹣m=0,方程的两实根为x1、x2,且x12+x22﹣x1x2=7,
∴ ![]() ,
,
∴(m﹣3)2﹣3×(﹣m)=7,
解得,m1=1,m2=2,
即m的值是1或2
【解析】(1)要证明方程有两个不相等的实数根,只要证明原来的一元二次方程的△的值大于0即可;(2)根据根与系数的关系可以得到关于m的方程,从而可以求得m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为km.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+b2 , 其中正确结论是(填序号)
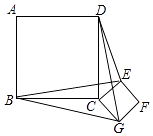
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“宏扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:

(1)如图,希望参加活动C占20%,希望参加活动B占15%,则被调查的总人数为人,扇形统计图中,希望参加活动D所占圆心角为度,根据题中信息补全条形统计图.
(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx(k为常数,k≠0)与双曲线y=
 (m为常数,m>0)的交点为A、B,AC⊥x轴于点C,∠AOC=30°,OA=2
(m为常数,m>0)的交点为A、B,AC⊥x轴于点C,∠AOC=30°,OA=2 
(1)求m、k的值;
(2)点P在y轴上,如果S△ABP=3k,求P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.

(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
相关试题

