【题目】如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q.

(1)试证明:无论点P运动到AB上何处时,都有△ADQ≌△ABQ;
(2)当点P在AB上运动到什么位置时,△ADQ的面积是正方形ABCD面积的![]() ;
;
(3)若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,当点P运动到什么位置时,△ADQ恰为等腰三角形.
参考答案:
【答案】(1)证明见解析;(2)AP=2;(3)P在B点,C点,或在CP=4(![]() -1)处,△ADQ是等腰三角形.
-1)处,△ADQ是等腰三角形.
【解析】
试题分析:(1)可由SAS求得△ADQ≌△ABQ;
(2)过点Q作QE⊥AD于E,QF⊥AB于F,则QE=QF,若△ADQ的面积是正方形ABCD面积的![]() ,则有S△ADQ=
,则有S△ADQ=![]() ADQE=
ADQE=![]() S正方形ABCD,求得OE的值,再利用△DEQ∽△DAP有
S正方形ABCD,求得OE的值,再利用△DEQ∽△DAP有![]() ,解得AP值;
,解得AP值;
(3)点P运动时,△ADQ恰为等腰三角形的情况有三种:有QD=QA或DA=DQ或AQ=AD.由正方形的性质知,①当点P运动到与点B重合时,QD=QA,此时△ADQ是等腰三角形,②当点P与点C重合时,点Q与点C也重合,此时DA=DQ,△ADQ是等腰三角形,③当AD=AQ=4时,有CP=CQ,CP=AC-AD而由正方形的对角线的性质得到CP的值.
试题解析:(1)在正方形ABCD中,
无论点P运动到AB上何处时,都有
AD=AB,∠DAQ=∠BAQ,AQ=AQ,
∴△ADQ≌△ABQ;
(2)△ADQ的面积恰好是正方形ABCD面积的![]() 时,
时,
过点Q作QE⊥AD于E,QF⊥AB于F,则QE=QF,

∵在边长为4的正方形ABCD中,
∴S正方形ABCD=16,
∴![]() AD×QE=
AD×QE=![]() S正方形ABCD=
S正方形ABCD=![]() ×16=
×16=![]() ,
,
∴QE=![]() ,
,
∵EQ∥AP,
∴△DEQ∽△DAP,
∴![]() ,即
,即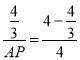 ,
,
解得AP=2,
∴AP=2时,△ADQ的面积是正方形ABCD面积的![]() ;
;
(3)若△ADQ是等腰三角形,则有QD=QA或DA=DQ或AQ=AD,
①当AD=DQ时,则∠DQA=∠DAQ=45°
∴∠ADQ=90°,P为C点,
②当AQ=DQ时,则∠DAQ=∠ADQ=45°,
∴∠AQD=90°,P为B,
③AD=AQ(P在BC上),
∴CQ=AC-AQ=![]() BC-BC=(
BC-BC=(![]() -1)BC
-1)BC
∵AD∥BC
∴![]() ,即可得
,即可得![]() =1,
=1,
∴CP=CQ=(![]() -1)BC=4(
-1)BC=4(![]() -1)
-1)
综上,P在B点,C点,或在CP=4(![]() -1)处,△ADQ是等腰三角形.
-1)处,△ADQ是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读理解)对于任意正实数a、b,
∵(
 ﹣
﹣ )2≥0,
)2≥0,∴a﹣2
 +b≥0,
+b≥0,∴a+b≥2
 ,(只有当a=b时,a+b等于2
,(只有当a=b时,a+b等于2 ).
).(1)(获得结论)在a+b≥2
 (a、b均为正实数)中,若ab为定值p,
(a、b均为正实数)中,若ab为定值p,则a+b≥2
 ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2 .
.根据上述内容,回答下列问题:若m>0,只有当m= 时,m+
 有最小值 .
有最小值 .(2)(探索应用)已知点Q(﹣3,﹣4)是双曲线y=
 上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=
上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y= (x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
(x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.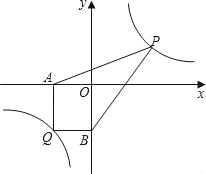
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上
 、
、 两点分别表示有理数
两点分别表示有理数 和
和 ,我们用
,我们用 表示
表示 到
到 之间的距离;例如
之间的距离;例如 表示7到3之间的距离.
表示7到3之间的距离.(1)当
 时,
时, 的值为 .
的值为 .(2)如何理解
 表示的含义?
表示的含义?(3)若点
 、
、 在0到3(含0和3)之间运动,求
在0到3(含0和3)之间运动,求 的最小值和最大值.
的最小值和最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象为直线l1,经过A(0,4)和D(4,0)两点,一次函数y=
 x+1的图象为直线l2,与x轴交于点C,两直线l1,l2相交于点B.
x+1的图象为直线l2,与x轴交于点C,两直线l1,l2相交于点B.(1)求k,b的值;
(2)求点B的坐标;
(3)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一位农民带上若干千克自产的土豆进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)求出降价前每千克的土豆价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方形ABCD中,点E是BC边上一点,且BE:EC=2:1,AE与BD交于点F,则△AFD与四边形DFEC的面积之比是________.
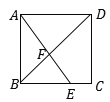
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了倡导“节约用水,从我做起”,市政府决定对市直机关500户家庭的用水情况做一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨)并将调查结果制成了如图所示的条形统计图。
(1)请将条形统计图补充完整;
(2)求这100个样本数据的平均数,众数和中位数;
(3)根据样本数据,估计市直机关500户家庭中平均用水量不超过12吨的约有多少户?

相关试题

