【题目】如图,一次函数y=kx+b的图象为直线l1,经过A(0,4)和D(4,0)两点,一次函数y=![]() x+1的图象为直线l2,与x轴交于点C,两直线l1,l2相交于点B.
x+1的图象为直线l2,与x轴交于点C,两直线l1,l2相交于点B.
(1)求k,b的值;
(2)求点B的坐标;
(3)求△ABC的面积.

参考答案:
【答案】(1)k=-1,b=4;(2) ![]() ;(3)
;(3) ![]()
【解析】
(1)把点A和点D的坐标分别代入y=kx+b得到关于k、b的方程组,然后解方程求出k、b的值;
(2)根据两直线相交的问题,通过解方程组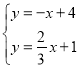 ,得到点B的坐标;
,得到点B的坐标;
(3)先确定C点坐标,然后利用△ABC的面积=S△ACD﹣S△BCD进行计算.
解:(1)把A(0,4)和D(4,0)分别代入y=kx+b得![]() ,解得
,解得![]() ;
;
(2)由(1)得一次函数的解析式为:y=﹣x+4,
解方程组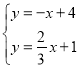 得
得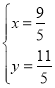 ,
,
所以点B的坐标为![]() ;
;
(3)当y=0时,![]() ,
,
解得x=![]() ,
,
则C点坐标为(![]() ,0),
,0),
所以△ABC的面积=S△ACD﹣S△BCD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数y=
 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.(1)求k的值;
(2)点N(a,1)是反比例函数y=
 (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读理解)对于任意正实数a、b,
∵(
 ﹣
﹣ )2≥0,
)2≥0,∴a﹣2
 +b≥0,
+b≥0,∴a+b≥2
 ,(只有当a=b时,a+b等于2
,(只有当a=b时,a+b等于2 ).
).(1)(获得结论)在a+b≥2
 (a、b均为正实数)中,若ab为定值p,
(a、b均为正实数)中,若ab为定值p,则a+b≥2
 ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2 .
.根据上述内容,回答下列问题:若m>0,只有当m= 时,m+
 有最小值 .
有最小值 .(2)(探索应用)已知点Q(﹣3,﹣4)是双曲线y=
 上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=
上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y= (x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
(x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.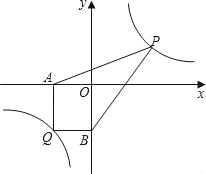
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上
 、
、 两点分别表示有理数
两点分别表示有理数 和
和 ,我们用
,我们用 表示
表示 到
到 之间的距离;例如
之间的距离;例如 表示7到3之间的距离.
表示7到3之间的距离.(1)当
 时,
时, 的值为 .
的值为 .(2)如何理解
 表示的含义?
表示的含义?(3)若点
 、
、 在0到3(含0和3)之间运动,求
在0到3(含0和3)之间运动,求 的最小值和最大值.
的最小值和最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q.

(1)试证明:无论点P运动到AB上何处时,都有△ADQ≌△ABQ;
(2)当点P在AB上运动到什么位置时,△ADQ的面积是正方形ABCD面积的
 ;
;(3)若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,当点P运动到什么位置时,△ADQ恰为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一位农民带上若干千克自产的土豆进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)求出降价前每千克的土豆价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?

-
科目: 来源: 题型:
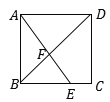
查看答案和解析>>【题目】如图所示,在正方形ABCD中,点E是BC边上一点,且BE:EC=2:1,AE与BD交于点F,则△AFD与四边形DFEC的面积之比是________.
相关试题

